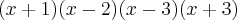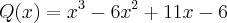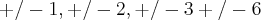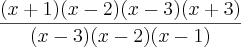por joaoalbertotb » Seg Ago 31, 2009 14:41
por joaoalbertotb » Seg Ago 31, 2009 14:41
Não compreendi muito bem o que tem q fazer
Resolva as equações a seguir pelo método de completar quadrados encontrando a raiz positiva da equação. Explique o que deverá ser feito para se obter as duas raízes sem utilizar a fórmula de Bháskara.
x2 + 10x + 16 = 7
x2 + bx + 9 = 0
x2 + 4x + c = 0
x2 + bx + c = 0
ax2 + bx + c = 0
desde ja obrigado
-
joaoalbertotb
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 25, 2009 11:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licensiatura
- Andamento: cursando
 por Molina » Seg Ago 31, 2009 18:37
por Molina » Seg Ago 31, 2009 18:37
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cristina » Sex Set 04, 2009 20:46
por cristina » Sex Set 04, 2009 20:46
Olá estou com uma dificuldade em resolver este exercicio... preciso de ajuda.....
Ao simplificar a fração algébrica

, quando

,
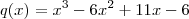
e
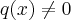
, obtemos a seguinte expressão:
a)

b)

c)

d)
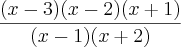
Não estou conseguindo simplificar esta expressão, qual é o passo correto????????
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Cleyson007 » Dom Set 06, 2009 11:02
por Cleyson007 » Dom Set 06, 2009 11:02
Cristina, primeiramente, descubra quais são as raizes de P(x) e de Q(x)
Assim, é só pesquisar quais são as raizes racionais de cada um dos polinômios, veja:

suas possíveis raizes são:
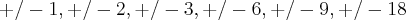
Substituindo no polinomio P(x) você verá que as raizes serão:

. Ou seja:
P(x)=
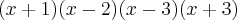
Vamos achar as raízes reais agora de Q(x):
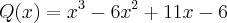
Suas possíveis raizes poderão ser:
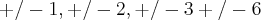
Substituindo no polinômio você verá que as raízes serão:

Então,

Fazendo

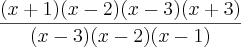
Simplificando a resposta será:
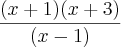
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda Urgente com esse problema de função
por Mayedra » Ter Nov 17, 2015 16:33
- 0 Respostas
- 1636 Exibições
- Última mensagem por Mayedra

Ter Nov 17, 2015 16:33
Funções
-
- Como resolvo esse problema envolvendo equação?
por LuizCarlos » Ter Jul 26, 2011 17:15
- 2 Respostas
- 4549 Exibições
- Última mensagem por LuizCarlos

Ter Jul 26, 2011 18:30
Sistemas de Equações
-
- como resolvo esse problema de sistema de equação?
por kellen e winicius » Ter Ago 30, 2011 00:13
- 3 Respostas
- 5080 Exibições
- Última mensagem por Caradoc

Ter Ago 30, 2011 20:50
Sistemas de Equações
-
- Problema com equação, ajuda
por LuizCarlos » Ter Jul 12, 2011 20:09
- 2 Respostas
- 1737 Exibições
- Última mensagem por Fabio Cabral

Qua Jul 13, 2011 10:16
Sistemas de Equações
-
- Problema envolvendo equação, ajuda !
por LuizCarlos » Qui Jul 28, 2011 15:04
- 1 Respostas
- 1435 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



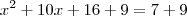
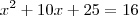
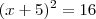

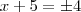
 e
e 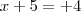
 e
e 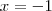


 , quando
, quando  ,
, 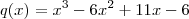 e
e 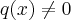 , obtemos a seguinte expressão:
, obtemos a seguinte expressão:


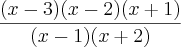


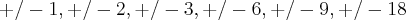
 . Ou seja:
. Ou seja: