 por Andreza » Qua Fev 22, 2012 12:35
por Andreza » Qua Fev 22, 2012 12:35
Tendo a primeira equação:
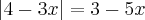
resolvi ela e encontrei as raízes x=-

e x=

Tendo a segunda equação

=0
Passei o 3 para o lado direito trocando o sinal e resolvi ela encontrando as raízes x= +
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
e x= -
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
.
Então pediu o produto das raízes reais eu multipliquei tudo e encontrei

.
Só q nao consigo achar o erro pois no gabarito a resposta é 1.
Desde já agradeço.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por timoteo » Qua Fev 22, 2012 15:51
por timoteo » Qua Fev 22, 2012 15:51
andreza eu impus a condiçao de existencia e as raizes que sao validas sao -1/2 e +- raiz de 2. multiplicando
![\sqrt[]{2} . -\sqrt[]{2} = -2 \sqrt[]{2} . -\sqrt[]{2} = -2](/latexrender/pictures/c56efbc3ed28ea9b6e488d3551f3e97a.png)
. fazendo -2 . -1/2= 1
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equações modulares
por Andreza » Qui Nov 24, 2011 13:11
- 1 Respostas
- 1685 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 20:55
Sistemas de Equações
-
- Inequacoes Modulares
por rousseau » Qui Abr 12, 2012 23:15
- 1 Respostas
- 1781 Exibições
- Última mensagem por rousseau

Qui Abr 12, 2012 23:26
Álgebra Elementar
-
- inequações modulares
por Alerecife » Ter Set 25, 2012 22:37
- 1 Respostas
- 1768 Exibições
- Última mensagem por MarceloFantini

Ter Set 25, 2012 23:20
Funções
-
- Inequações Modulares
por augustokuc » Qua Set 11, 2013 18:32
- 0 Respostas
- 1478 Exibições
- Última mensagem por augustokuc

Qua Set 11, 2013 18:32
Inequações
-
- INEQUAÇÕES MODULARES
por petras » Ter Jun 14, 2016 17:15
- 1 Respostas
- 3281 Exibições
- Última mensagem por petras

Seg Out 31, 2016 21:15
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
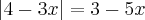
 e x=
e x=
 =0
=0![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e x= -
e x= - ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) .
. .
.

![\sqrt[]{2} . -\sqrt[]{2} = -2 \sqrt[]{2} . -\sqrt[]{2} = -2](/latexrender/pictures/c56efbc3ed28ea9b6e488d3551f3e97a.png) . fazendo -2 . -1/2= 1
. fazendo -2 . -1/2= 1