Olá! sou novo por aqui. enfim!
Tenho duvida nessa questão: Já tentei varias vezes, bom sei que ela pode ser resolvida por "escalonamento"´. O que eu devo estar confundindo é na hora de cancelar uma icognita x,y ou z.
1º) Sabendo que (x,y,z) é solução do sistema.
x+y+z=1
x-y+2z=3 , o valor de x²+y²+z² é:
2x+3y-z=1
Obrigado, pela atenção estarei fazendo novas perguntas!
Obs: não sei por "Chaves" do lado esquerdo do sistema.


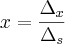
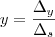
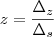
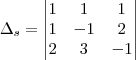
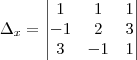
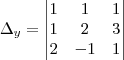
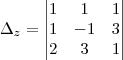



 ,
,  e
e  formam uma matriz incompleta.
formam uma matriz incompleta.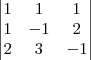 Encontrará como resultado
Encontrará como resultado 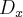 ).
).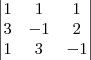 Encontrará como resultado
Encontrará como resultado 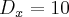
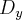 fica:
fica: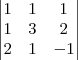

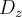 fica:
fica: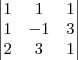 Encontrará como resultado:
Encontrará como resultado: 
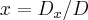 ,
, 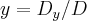 e
e 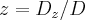 .
.


 .
.
 :
: