 por LuizCarlos » Seg Jul 25, 2011 14:07
por LuizCarlos » Seg Jul 25, 2011 14:07
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 14:47
por Molina » Seg Jul 25, 2011 14:47
Boa tarde, Luiz Carlos.
Você fez tudo correto, só se esqueceu que da parte que parou, basta multiplicar cruzado, saindo assim das frações.
Lembre-se que:
 (multiplicação cruzada)
(multiplicação cruzada)Qualquer dúvida, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Seg Jul 25, 2011 15:56
por LuizCarlos » Seg Jul 25, 2011 15:56
Molina escreveu:Boa tarde, Luiz Carlos.
Você fez tudo correto, só se esqueceu que da parte que parou, basta multiplicar cruzado, saindo assim das frações.
Lembre-se que:
 (multiplicação cruzada)
(multiplicação cruzada)Qualquer dúvida, informe!

Boa tarde, Molina, Obrigado por responder minha duvida!
Fiz aqui como você informou, será que é dessa forma?
Pois no final do livro, o resultado dessa questão é 1.
Olhe:
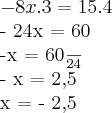
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 17:40
por Molina » Seg Jul 25, 2011 17:40
Boa tarde.
Passou despercebido por mim um equívoco seu, veja:
Na segunda fração, após fazer a distributiva, quando você expande a fração, o segundo termo fica positivo, pois há aquele sinal negativo na frente da fração.
O certo é:

Agora dá certo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Seg Jul 25, 2011 18:47
por LuizCarlos » Seg Jul 25, 2011 18:47
Molina escreveu:Boa tarde.
Passou despercebido por mim um equívoco seu, veja:
Na segunda fração, após fazer a distributiva, quando você expande a fração, o segundo termo fica positivo, pois há aquele sinal negativo na frente da fração.
O certo é:

Agora dá certo

blz, deu certo aqui, mas só que deu -1 negativo, sendo que a resposta no livro é 1 positivo.
Fiz dessa forma.
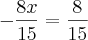
- 8x . 15 = 15 . 8
- 120x = 120
-x = \frac{120}{120}[/tex]
-x = 1
x = - 1
minha duvida é aqui
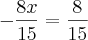
a duvida é, nesse caso do

esse sinal de menos vale tando para 8x como para 15?
ou seja entao o correto seria assim?
![- 8x . 15 = -15 . 8
- 120x = - 120
-x = [tex] \frac{-120}{120} - 8x . 15 = -15 . 8
- 120x = - 120
-x = [tex] \frac{-120}{120}](/latexrender/pictures/65b2ba6ea1c5975d965995bfd78d0566.png)
-x = -1
x = 1
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 19:19
por Molina » Seg Jul 25, 2011 19:19
Boa tarde.
LuizCarlos escreveu: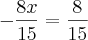
Você está cometendo um erro na adição e subtração das frações do lado direito da igualdade.
Veja que:
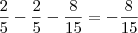
Ou seja, temos que:
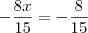
Chegando em

.
LuizCarlos escreveu:esse sinal de menos vale tando para 8x como para 15?
ou seja entao o correto seria assim?
Não está correto. O sinal de subtração é para um único número.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Seg Jul 25, 2011 19:39
por LuizCarlos » Seg Jul 25, 2011 19:39
Molina escreveu:Boa tarde.
LuizCarlos escreveu: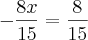
Você está cometendo um erro na adição e subtração das frações do lado direito da igualdade.
Veja que:
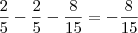
Ou seja, temos que:
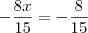
Chegando em

.
LuizCarlos escreveu:esse sinal de menos vale tando para 8x como para 15?
ou seja entao o correto seria assim?
Não está correto. O sinal de subtração é para um único número.

hum, entendi professora Molina.
Consegui resolver agora!
Mas quero quer voce me responda essa duvida !
quando eu tenho
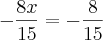
esse menos na frente das frações significa que apenas o numerador 8x é negativo, e o numerador 8 é negativo?
entao o denominador 15 é positivo, e o denominador 15 é positivo?
sempre que tiver frações assim, com menos na frente do traço da fração, apenas os numeradores são negativos?
estou fazendo confusão nisso!
obrigado professora
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Jul 25, 2011 19:54
por Molina » Seg Jul 25, 2011 19:54
Boa noite.
Primeira correção: Não sou professor
A, meu nome é
Diego Molina, ok?

Vamos a matemática...
Essa é uma dúvida bem rotineira, mas bem simples de se explicar:
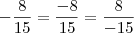
Ou seja, tanto faz onde que fica o sinal de igual, ele está simbolizando que aquela fração é negativa. Então pode ser a fração toda negativa (primeiro caso), o numerador negativo (segundo caso) ou o denominador negativo (terceiro caso). Essas três frações são as mesmas, independente de onde você colocar o sinal negativo.
Ficou mais claro agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Ter Jul 26, 2011 00:04
por LuizCarlos » Ter Jul 26, 2011 00:04
LuizCarlos escreveu:Molina escreveu:Boa tarde.
LuizCarlos escreveu: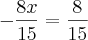
Você está cometendo um erro na adição e subtração das frações do lado direito da igualdade.
Veja que:
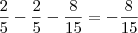
Ou seja, temos que:
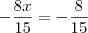
Chegando em

.
LuizCarlos escreveu:esse sinal de menos vale tando para 8x como para 15?
ou seja entao o correto seria assim?
Não está correto. O sinal de subtração é para um único número.

hum, entendi professora Molina.
Consegui resolver agora!
Mas quero quer voce me responda essa duvida !
quando eu tenho
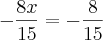
esse menos na frente das frações significa que apenas o numerador 8x é negativo, e o numerador 8 é negativo?
entao o denominador 15 é positivo, e o denominador 15 é positivo?
sempre que tiver frações assim, com menos na frente do traço da fração, apenas os numeradores são negativos?
estou fazendo confusão nisso!
obrigado professora
Opa, desculpa pelo engano professor Diego!
agora entendi perfeitamente, voce é otimo professor!
grato pela sua ajuda, e contribuição, continue sempre assim.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como eu resolvo essa questão
por diegoconain5 » Qua Jul 16, 2014 18:53
- 0 Respostas
- 1202 Exibições
- Última mensagem por diegoconain5

Qua Jul 16, 2014 18:53
Equações
-
- Ajudem-me. Como resolvo essa matriz.?
por danielvale28 » Ter Ago 11, 2009 08:55
- 2 Respostas
- 2496 Exibições
- Última mensagem por Cleyson007

Ter Ago 11, 2009 15:57
Matrizes e Determinantes
-
- Como resolvo essa integral indefinida??
por Justiceira » Sáb Out 31, 2009 19:52
- 3 Respostas
- 3073 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 21:06
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo essa função? ALGUÉM SABE?
por Kelvin Brayan » Qua Mai 25, 2011 13:12
- 3 Respostas
- 2762 Exibições
- Última mensagem por Kelvin Brayan

Qui Mai 26, 2011 10:58
Funções
-
- Por favor, como resolvo essa questão de função
por Ronaldobb » Qui Set 20, 2012 19:25
- 1 Respostas
- 1915 Exibições
- Última mensagem por MarceloFantini

Qui Set 20, 2012 21:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


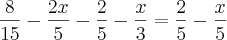

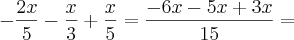

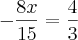



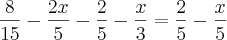

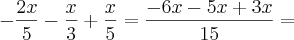

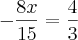

 (multiplicação cruzada)
(multiplicação cruzada)

(multiplicação cruzada)
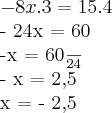




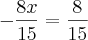
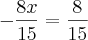

![- 8x . 15 = -15 . 8
- 120x = - 120
-x = [tex] \frac{-120}{120} - 8x . 15 = -15 . 8
- 120x = - 120
-x = [tex] \frac{-120}{120}](/latexrender/pictures/65b2ba6ea1c5975d965995bfd78d0566.png)

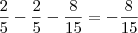
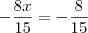
 .
.

.
LuizCarlos escreveu:esse sinal de menos vale tando para 8x como para 15?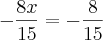

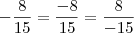


.
LuizCarlos escreveu:esse sinal de menos vale tando para 8x como para 15?
