Eu fiz essa questões de todas as maneiras possíveis e só consegui chegar ao resultado de 968690,9401242 porém a resposta correta é 968,690.
O que eu estou fazendo de errado?
1/ 6,28 x 0,8 x10^3 x 205,478 x10^-12



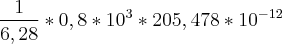
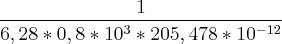

Gebe escreveu:Primeiramente a forma como tu colocou a expressão está confusa.
Dessa forma como está escrito é equivalente a:
Porem pelo resultado deve ser:
Sendo assim, realmente a tua conta está certa. Para bater com o gabarito falta um 1000 multiplicando no denominador, logo ou o gabarito está errado mesmo ou (uma possibilidade) o exercicio esta utilizando a virgula do 205,478 em outra notação, ou seja, é na verdade 205478 ou ainda o gabarito está apresentado neste tipo de notação (virgula separando os milhares das centenas).

Gebe escreveu:Primeiramente a forma como tu colocou a expressão está confusa.
Dessa forma como está escrito é equivalente a:
Porem pelo resultado deve ser:
Sendo assim, realmente a tua conta está certa. Para bater com o gabarito falta um 1000 multiplicando no denominador, logo ou o gabarito está errado mesmo ou (uma possibilidade) o exercicio esta utilizando a virgula do 205,478 em outra notação, ou seja, é na verdade 205478 ou ainda o gabarito está apresentado neste tipo de notação (virgula separando os milhares das centenas).

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: