 por luanxd » Ter Fev 09, 2010 23:44
por luanxd » Ter Fev 09, 2010 23:44
Resolver, em R a equação:
![\sqrt[3]{{x^2}+x-1}=x-1 \sqrt[3]{{x^2}+x-1}=x-1](/latexrender/pictures/7c3f09e903e892167979bb0d259d2228.png)
![{(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3} {(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3}](/latexrender/pictures/0c2c46ce73bd5cf9c29de898392b4930.png)
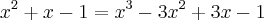
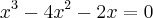
Não consegui ir adiante tenho quase certeza de que algo esta errado, poder me ajuda a encontrar o erro ,e me ajudar a terminar a equação.
Obrigado pela atenção!
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Fev 10, 2010 12:29
por Molina » Qua Fev 10, 2010 12:29
Fatora essa equacao do terceiro grau para ficar com uma do segundo grau.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Qua Fev 10, 2010 12:38
por MarceloFantini » Qua Fev 10, 2010 12:38
Bom dia Luan.
Está tudo certo, com exceção de um sinal:
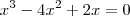
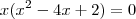
Daí:

Ou:
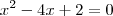
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação irracional
por Rosana Vieira » Ter Nov 29, 2011 13:51
- 1 Respostas
- 1608 Exibições
- Última mensagem por ivanfx

Ter Nov 29, 2011 15:04
Funções
-
- Equação irracional
por PeterHiggs » Sex Set 28, 2012 12:33
- 2 Respostas
- 1564 Exibições
- Última mensagem por PeterHiggs

Sex Set 28, 2012 22:14
Álgebra Elementar
-
- Equação irracional
por Flordelis25 » Sáb Abr 20, 2013 17:39
- 2 Respostas
- 1580 Exibições
- Última mensagem por Flordelis25

Sex Mai 24, 2013 17:17
Equações
-
- Equaçao Irracional
por Amanda91 » Qua Jul 10, 2013 03:05
- 3 Respostas
- 1829 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 02, 2013 09:14
Equações
-
- [Equação irracional]
por Victor985 » Qui Dez 12, 2013 20:37
- 1 Respostas
- 1128 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 13:38
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{{x^2}+x-1}=x-1 \sqrt[3]{{x^2}+x-1}=x-1](/latexrender/pictures/7c3f09e903e892167979bb0d259d2228.png)
![{(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3} {(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3}](/latexrender/pictures/0c2c46ce73bd5cf9c29de898392b4930.png)
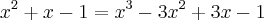
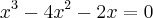

![\sqrt[3]{{x^2}+x-1}=x-1 \sqrt[3]{{x^2}+x-1}=x-1](/latexrender/pictures/7c3f09e903e892167979bb0d259d2228.png)
![{(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3} {(\sqrt[3]{{x^2}+x-1})^3}={(x-1)^3}](/latexrender/pictures/0c2c46ce73bd5cf9c29de898392b4930.png)
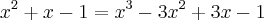
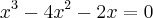


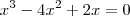
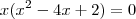

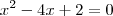


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.