 por filipe reis farias » Sáb Mai 18, 2013 15:28
por filipe reis farias » Sáb Mai 18, 2013 15:28
Boa tarde. Meu nome e filipe reis farias.
Galera, estou com duvide de como resolver esse exercicio de sistema linear, observem"
1)Tres amigos, Alberto, Bento e Cesar, colecionam figurinhas de jogadores de futebol das selecoes da Copa do mundo. Descubra a quantidade de figurinhas que cada um possui apartir das informacoes seguintes.
-> Se Alberto der a Bento cinco figurinhas, eles passarao a ter a mesma quantidade.
-> Se Bento perder 25% de seu total de figurinhas, ficara com cinco figurinhas a menos que Cesar.
-> Se Cesar receber a decima parte das figurinhas de alberto, ficara com a mesma quantidade que bento.
Bom, Como o forum quer que eu mostre a minha tentativa de resolucao, entao vamos la:
Eu Interpretei assim, observem:
A-5 = B+5
B-B/4 = C-5
C+A/10 = B
Eu tentei pelo metodo de substituicao, porem, nao deu certo. Depois tentei escalonar e acabou dando errado, tambem.
Ajudem-me
filipe reis farias.[color=#4000FF][/color]
-
filipe reis farias
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 15, 2013 23:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursando 3 ano do ensino media. somente.
- Andamento: cursando
 por DanielFerreira » Dom Mai 19, 2013 20:03
por DanielFerreira » Dom Mai 19, 2013 20:03
Filipe,
boa noite! Seja bem-vindo!!
Interpretou corretamente!
Acredito que pelo método da substituição seja o mais simples, veja:
Equação I:

Equação II:
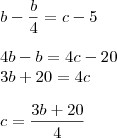
Equação III:

Creio que consegue finalizar. Caso contrário, retorne!!
Att,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicios de sistemas lineares!Estou tentando resolver,mas.
 por boskim22 » Sex Jun 03, 2011 16:46
por boskim22 » Sex Jun 03, 2011 16:46
- 0 Respostas
- 1418 Exibições
- Última mensagem por boskim22

Sex Jun 03, 2011 16:46
Sistemas de Equações
-
- [Sistemas Lineares] Dúvida simples
por rnts » Qua Abr 04, 2012 12:04
- 1 Respostas
- 1637 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 19:26
Matrizes e Determinantes
-
- [Sistemas Lineares] Duvida sobre classificacao!
 por filipe reis farias » Sáb Mai 18, 2013 15:09
por filipe reis farias » Sáb Mai 18, 2013 15:09
- 1 Respostas
- 6238 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 20:24
Sistemas de Equações
-
- [ESCALONAMENTO] como resolver esses sistemas
 por mayconlucas » Seg Nov 09, 2015 09:39
por mayconlucas » Seg Nov 09, 2015 09:39
- 2 Respostas
- 3540 Exibições
- Última mensagem por nakagumahissao

Ter Nov 10, 2015 15:31
Álgebra Linear
-
- [Sistemas lineares] Fiquei com uma dúvida na resolução desse
por Aprendiz2012 » Sáb Ago 11, 2012 18:27
- 2 Respostas
- 1842 Exibições
- Última mensagem por Aprendiz2012

Sáb Ago 11, 2012 20:37
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



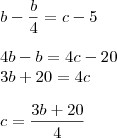




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.