 por Samambass » Seg Ago 23, 2010 11:45
por Samambass » Seg Ago 23, 2010 11:45
Estou com muita dificuldade para discutir o sistema abaixo em função do parâmetro
k, ou seja:
Preciso classifica-los, quanto ao número de soluções dizendo se são: Determinado, indeterminado, impossível, etc.
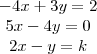
Obs.: Estou tentando pelo método de escalonamento de matriz, isso está correto ou é por outro método? Por favor, poderiam me ajudar?
-
Samambass
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Ago 23, 2010 11:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado/Engenharia Mecatrônica
- Andamento: cursando
 por alexandre32100 » Sex Set 24, 2010 01:39
por alexandre32100 » Sex Set 24, 2010 01:39
Nunca gostei muito da resolução de sistemas por matrizes, e também não creio que seja este o caminho.
Primeiramente resolveremos somente as primeiras duas equações do sistema, assim:

Escolha qual método quer utilizar, mas a resposta é

e
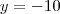
.
Aplique esta resposta à terceira equação:

.

Aqui pode-se de ver que, se

o sistema é impossível no conjunto

, para qualquer outro valor, o sistema é definido, admite apenas a solução
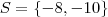
.
-
alexandre32100
-
 por filipepaixao » Qua Set 29, 2010 10:19
por filipepaixao » Qua Set 29, 2010 10:19
Eu realmente ando a aprender resolver sistemas de equações Lineares (grandes dores de cabeça)
A minha questão seria a seguinte com esse sistema seria possivel começar por usar o Método de Eliminação de Gauss?
ou não é possivel colocar numa matriz visto que não daria uma matriz quadrada?
Ainda estou muito "fresquinho" nesta matéria desculpem a minha "ignorância"...
Obs. Algo que me ajude a perceber essa matéria agradecia.
Abraço
-

filipepaixao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 29, 2010 09:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Programação de Sistemas
- Andamento: cursando
 por alexandre32100 » Qui Set 30, 2010 13:08
por alexandre32100 » Qui Set 30, 2010 13:08
Pois é. Creio que o sistema de eliminação não seja o método mais simples nesta questão.
filipepaixao escreveu:não é possivel colocar numa matriz visto que não daria uma matriz quadrada
Na verdade podemos formar uma matriz quadrada se pensarmos o sistema dessa forma:

Por fim, resolve-se o sistema -
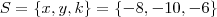
, e então conclui-se o problema.
-
alexandre32100
-
 por MarceloFantini » Qui Set 30, 2010 19:32
por MarceloFantini » Qui Set 30, 2010 19:32
Só porque não é uma matriz quadrada não quer dizer que não pode ser colocado numa matriz. A questão é que essa matriz apenas não serviria pra muita coisa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por filipepaixao » Sáb Out 02, 2010 09:14
por filipepaixao » Sáb Out 02, 2010 09:14
Agradecido alexandre32100.
Abraço
-

filipepaixao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 29, 2010 09:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Programação de Sistemas
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3084 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5551 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4491 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2671 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
-
- Sistema Linear
por kael » Qua Out 21, 2009 13:43
- 1 Respostas
- 3635 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2009 15:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
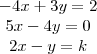

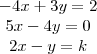


 e
e 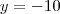 .
. .
.
 o sistema é impossível no conjunto
o sistema é impossível no conjunto  , para qualquer outro valor, o sistema é definido, admite apenas a solução
, para qualquer outro valor, o sistema é definido, admite apenas a solução 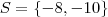 .
.

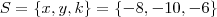 , e então conclui-se o problema.
, e então conclui-se o problema.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
