estou com um problema para simplificar o seguinte exercicio. Já tentei algumas vezes mais não consegui =/
gostaria que me ajudassem, ficarei muito grato.

Abraços.




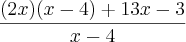
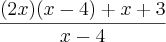



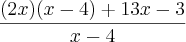
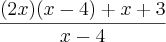
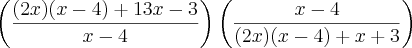
 que é comum tanto no numerador como no denominador, temos:
que é comum tanto no numerador como no denominador, temos: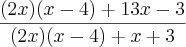
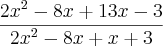
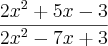
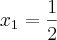

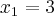
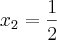
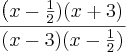



Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



