Sistemas Lineares

[Cleyson007]

Olá, tudo bem?
Gostaria de saber se o modo que eu utilizei para resolver esse sistema linear está correto. Desde já agradeço, que Deus lhe abençoe.

O sistema é o seguinte:

2x-y+z=4 I
x+2y+z=1 II
x+y+2z=3 III

Da I com a II: Adicionei -2 a II equação para cortar o x, obtendo a equação: -5y-z=2 IV
Da I com a III: Em seguida adicionei -2 a III para cortar o x, obtendo a equação: -3y-3z=-2 IV
Da IV com a V: Adicionei 3 a IV equação para cortar o z, obtendo y= -2/9.
Substitui o valor de y na IV equação achando z= -28/9.
Substitui os valores de z e y na I equação, obtendo x= 31/9.
S:(31/9,-2/9,-28/9)

[admin]

Olá Cleyson, boa noite, tudo bem!

Da I com a II: Adicionei -2 a II equação para cortar o x, obtendo a equação: -5y-z=2 IV

Aqui, não é verdade que você adicionou -2 à equação II, de fato, você multiplicou por -2 os dois membros da equação II e em seguida somou as equações I e II, obtendo sua equação IV.

Da I com a III: Em seguida adicionei -2 a III para cortar o x, obtendo a equação: -3y-3z=-2 IV

Aqui vale o mesmo comentário, você multiplicou por -2 a equação III e somou com a equação I, obtendo a equação V.

Da IV com a V: Adicionei 3 a IV equação para cortar o z, obtendo y= -2/9.

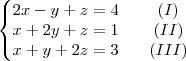
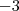Cleyson, acredito que aqui sua intenção foi multiplicar por os dois membros da equação IV e somá-la com a equação V, assim poderá obter pois .
Refaça as contas a partir deste passo para obter a solução.


Vale ressaltar que há vários modos de resolver.
Inclusive, o sistema pode ser escrito na forma matricial, como o produto entre duas matrizes.
O método que você está utilizando é de escalonamento, pois obtém um outro sistema equivalente, já escalonado.
Veja um exemplo de sistema equivalente ao inicial, escalonado:

A partir daqui, a solução pode ser obtida por substituição.


Comente qualquer dúvida.
Espero ter ajudado!

[Cleyson007]

Olá Fábio Sousa, realmente quando eu disse: Da IV com a V: Adicionei 3 a IV equação para cortar o z, obtendo y= -2/9, descuidei-me, a intenção era de multiplicar por -3.
Aqui a refaço de novo:
-5y-z=2 IV
-3y-3z=-2 V
Multipliquei por -3 a equação IV para cortar o z, e achei o valor de y= -2/3.
Substituindo y na IV equação encontrei z= 4/3.
Substituindo os valores de y e z na I equação encontrei x= 1.
Espero que seja isso!!! S: (1, -2/3, 4/3).
Muito obrigado por me ajudar em meus estudos, que Deus lhe abençoe.
Um forte abraço, boa noite.

[admin]

Olá Cleyson!

Também obtive este conjunto-solução.
Apenas completando um comentário anterior sobre a forma matricial, este sistema também pode ser escrito assim, considerando a definição de produto de matrizes:




Como o número de equações é igual ao número de incógnitas, também podemos resolver através de determinantes, pelo teorema de Cramer, considerando o determinante da matriz dos coeficientes que é quadrada:



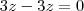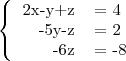
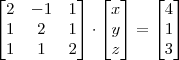
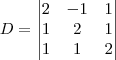
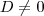Se , o sistema tem solução única 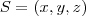, sendo: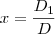








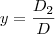
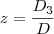
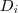Onde é o determinante da matriz obtida a partir da matriz dos coeficientes, substituindo-se a i-ésima coluna pela coluna dos termos independentes das equações do sistema.

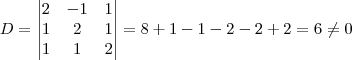(então, o sistema possui solução única)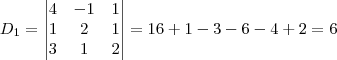









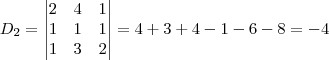
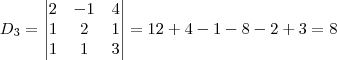
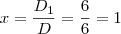
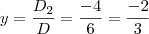
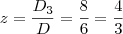
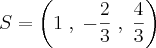
Então, confirmando a solução já obtida:









Vale estudar o teorema de Cramer, especialmente para resolver sistemas lineares com mais de 3 equações.
Bons estudos!