 , então:
, então:V=(1)
V=(-1,0,1)
V=(-1,1)
V=(-1,1)
V=(0)
Por favor me ajudem a resolver está equação.

luanxd escreveu:Dada a equação, então:
V=(1)
V=(-1,0,1)
V=(-1,1)
V=(-1,1)
V=(0)
Por favor me ajudem a resolver está equação.





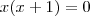
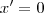

 e
e  seriam as soluções da equação. Porém, temos que
seriam as soluções da equação. Porém, temos que  não pode ser solução do sistema, já que substituindo-o os denominadores da fração ficam igual a zero (o que não pode).
não pode ser solução do sistema, já que substituindo-o os denominadores da fração ficam igual a zero (o que não pode).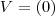



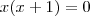

luanxd escreveu:Ola Molina obrigado pela ajuda, mas eu não entendi muito bem o finalzinho.
Como você acho o X1 eo X2?
Obrigado pela atenção.

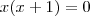
 e
e  que multiplicados dão zero. Como o produto é 0, ou o primeiro é igual a 0 ou o segundo é igual a 0. E foi isso que eu fiz:
que multiplicados dão zero. Como o produto é 0, ou o primeiro é igual a 0 ou o segundo é igual a 0. E foi isso que eu fiz: (ou seja, o primeiro termo desse produto é igual a zero)
(ou seja, o primeiro termo desse produto é igual a zero)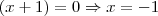



Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)