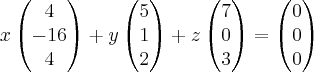
onde x, y e z são números reais. É verdade que:
a) a equação admite uma solução
b) em qualquer solução,
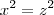
c) em qualquer solução,
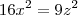
d) em qualquer solução,
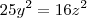
e) em qualquer solução,
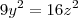
Eu já tentei resolvê-lo várias vezes e não consegui.
por Victor985 » Dom Nov 03, 2013 18:16
por e8group » Seg Nov 04, 2013 19:22
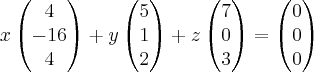
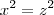
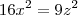
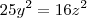
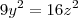
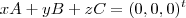. (A,B,C são as mesmas matrizes colunas dadas )
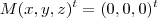, onde 
é uma matriz 
em que suas colunas 1,2,3 são respectivamente as matrizes colunas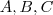 
. 
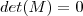, veja não é invertível o que implica que o sistema é incompatível (não há solução ) ou compatível indeterminado (infinitas soluções ) , mas como todo sistema linear homogêneo possui pelo menos a solução trivial que é o vetor nulo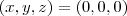 
,então por ser singular , concluímos que o sistema em questão é compatível e indeterminado (possui infinitas soluções ) . Aqui já eliminamos o item (a) .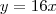 
e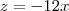 
. Mas faça as contas .
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.