alguém poderia me ajudar com essa dúvida ..
como saber quando um sistema é possível e determinado ?
possível e indeterminado?
sistema impossível ?



 o sistema é impossível.
o sistema é impossível.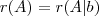 o sistema é possível.
o sistema é possível.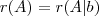 e ngl = 0, o sisteme é possível e determinado.
e ngl = 0, o sisteme é possível e determinado.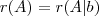 e ngl >0, o sistema é possível mas indeterminado
e ngl >0, o sistema é possível mas indeterminado
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
