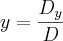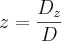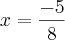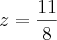por sandi » Sáb Set 26, 2009 22:17
por sandi » Sáb Set 26, 2009 22:17
2x + y + 3z = 4
x - y + 2z = 1
4x + y + z = 0
me ajudem a resolver..ainda to com dificuldades
-
sandi
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sáb Set 26, 2009 01:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: cursando
 por marciommuniz » Dom Set 27, 2009 01:01
por marciommuniz » Dom Set 27, 2009 01:01
sandi escreveu:2x + y + 3z = 4
x - y + 2z = 1
4x + y + z = 0
me ajudem a resolver..ainda to com dificuldades
Olá, utilize o método de escalonamento de Gaus..
é muito util
coloque cada incognita em colunas e uma coluna para os valores
assim:
2 1 3 4
1 -1 2 1
4 1 1 0
Agora some, multiplique ou divida linhas na matriz para fazer com que a matriz fique escalonada.
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por sandi » Dom Set 27, 2009 02:10
por sandi » Dom Set 27, 2009 02:10
valew..vou tentar..

-
sandi
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sáb Set 26, 2009 01:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração
- Andamento: cursando
 por Cleyson007 » Dom Set 27, 2009 11:21
por Cleyson007 » Dom Set 27, 2009 11:21
Bom dia Sandi!
Gosto de usar a Regra de Cramer..
Inicialmente, calcula-se
D, o determinante da matriz dos coeficientes do sistema.

Resolvendo, D = 16.
Em seguida, calcula-se
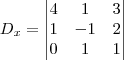
Resolvendo,

.
Em seguida, calcula-se
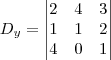
Resolvendo,

.
Em seguida, calcula-se

Resolvendo,
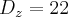
.
--> O valor de cada incógnita é o quociente de cada um desses determinantes por D, ou seja:

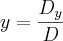
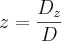
Logo,
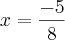

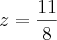
Comente qualquer dúvida.

Até mais.
Bons estudos!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Solução de Sistema
por yonara » Ter Jun 30, 2009 19:19
- 6 Respostas
- 11391 Exibições
- Última mensagem por Cleyson007

Sáb Jul 11, 2009 14:45
Sistemas de Equações
-
- solução de sistema
por sandi » Sáb Set 26, 2009 02:44
- 3 Respostas
- 5936 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:18
Sistemas de Equações
-
- Resolver com sistema de solução
por Tobias » Dom Mai 18, 2014 16:24
- 1 Respostas
- 2137 Exibições
- Última mensagem por Desu

Qui Mai 22, 2014 22:56
Trigonometria
-
- Solução de sistema - Ensino Médio
por bpepperoni » Sex Mar 11, 2011 15:50
- 1 Respostas
- 3071 Exibições
- Última mensagem por LuizAquino

Sex Mar 11, 2011 17:30
Sistemas de Equações
-
- [Matriz]Conjunto Solucao do sistema
por leonardoxx » Sex Nov 16, 2012 12:38
- 3 Respostas
- 4202 Exibições
- Última mensagem por e8group

Dom Nov 18, 2012 17:21
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







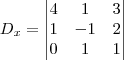
 .
.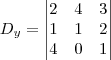
 .
.
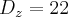 .
.