(I) A solução da inequação
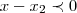 é o intervalo (0, 1]
é o intervalo (0, 1](II) A solução da inequação
 é o intervalo (-1, 1)
é o intervalo (-1, 1) (2,infinito)
(2,infinito)
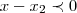 é o intervalo (0, 1]
é o intervalo (0, 1] é o intervalo (-1, 1)
é o intervalo (-1, 1) (2,infinito)
(2,infinito)



 é o intervalo:
é o intervalo: ![]-\infty,0[\cup]1,+\infty[ ]-\infty,0[\cup]1,+\infty[](/latexrender/pictures/cec5d89ffdd580d5ba482f8daaab75ea.png)
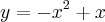 tem a concavidade voltada para baixo.
tem a concavidade voltada para baixo.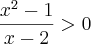
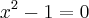
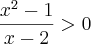 é o intervalo:
é o intervalo: ![]-1,1[\cup]2,+\infty[ ]-1,1[\cup]2,+\infty[](/latexrender/pictures/e26e07ea83eedd62898da252e7103b28.png)


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.