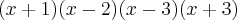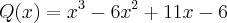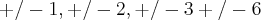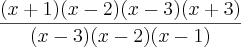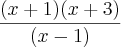Não compreendi muito bem o que tem q fazer
Resolva as equações a seguir pelo método de completar quadrados encontrando a raiz positiva da equação. Explique o que deverá ser feito para se obter as duas raízes sem utilizar a fórmula de Bháskara.
x2 + 10x + 16 = 7
x2 + bx + 9 = 0
x2 + 4x + c = 0
x2 + bx + c = 0
ax2 + bx + c = 0
desde ja obrigado



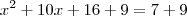
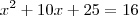
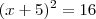

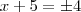
 e
e 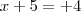
 e
e 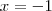


 , quando
, quando  ,
, 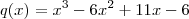 e
e 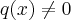 , obtemos a seguinte expressão:
, obtemos a seguinte expressão:


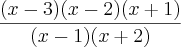


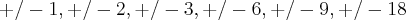
 . Ou seja:
. Ou seja: