


 sendo
sendo  o seu lado.
o seu lado.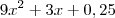 pode ser fatorado como
pode ser fatorado como 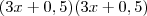 e portanto o lado do quadrado será
e portanto o lado do quadrado será 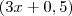
 então
então 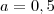



robson escreveu:ola boa noite essa equação esta correta
y+3=(-1/6).(x-2)
y+3=-1/6x +2/6
1/6x+y+3-2/6=0
x/6+y+3-1/3=0
x+6y+18-2/6=0
x+6y+18-2=0
x+6y+16=0










Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: