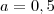por joaoalbertotb » Ter Set 01, 2009 14:08
por joaoalbertotb » Ter Set 01, 2009 14:08
1) O trinômio 9x²+3x+0,25 representa a medida da área de um quadrado.
O lado do quadrado mede a)1,5 b)3x+0,5 c)0,5
o termo 0,25 representa a medida da área de um quadrado cujo lado mede a)1,5 b)3x+0,5 c)0,5
o termo 3x representa a medida da área de dois retângulos.A medida da area de cada um mede a)1,5 b)3x+0,5 c)0,5
2)O trinômio 4x²+x+1/16 representa a área de um quadrado. O termo x representa a soma das áreas de dois retângulos. As medidas dos lados de um desses retângulos são expressas por:
a)4xe1/4
b)2xe1/4
c)xe1/4
3) o trinômio 0,25x²+0,5x+___ representa a área de um quadrado se o termo que falta for igual a 0,5.
a)verdadeiro
b)falso
-
joaoalbertotb
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Ago 25, 2009 11:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licensiatura
- Andamento: cursando
 por Marcampucio » Ter Set 01, 2009 15:57
por Marcampucio » Ter Set 01, 2009 15:57
1) a área de um quadrado é dada por

sendo

o seu lado.
o trinômio
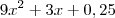
pode ser fatorado como
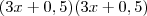
e portanto o lado do quadrado será
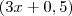
se

então
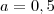
A figura abaixo faz a interpretação geométrica do trinômio:

os outros são do mesmo jeito.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por robson » Qua Set 02, 2009 21:57
por robson » Qua Set 02, 2009 21:57
ola boa noite essa equação esta correta
y+3=(-1/6).(x-2)
y+3=-1/6x +2/6
1/6x+y+3-2/6=0
x/6+y+3-1/3=0
x+6y+18-2/6=0
x+6y+18-2=0
x+6y+16=0
-
robson
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Set 02, 2009 21:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Marcampucio » Qui Set 03, 2009 01:08
por Marcampucio » Qui Set 03, 2009 01:08
robson escreveu:ola boa noite essa equação esta correta
y+3=(-1/6).(x-2)
y+3=-1/6x +2/6
1/6x+y+3-2/6=0
x/6+y+3-1/3=0
x+6y+18-2/6=0
x+6y+18-2=0
x+6y+16=0

Editado pela última vez por
Marcampucio em Qui Set 03, 2009 17:20, em um total de 1 vez.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Elcioschin » Qui Set 03, 2009 12:13
por Elcioschin » Qui Set 03, 2009 12:13
Marcampucio
A solução do Robson estava correta ----> x + 6y + 16 = 0
A sua solução ficou errada porque você inverteu o sinal de +3 para -3 na terceira linha.
De qualquer maneira, o caminho mais simples para chegar na solução é:
y + 3 = (-1/6)*(x - 2) ----> y + 3 = (1/-6)*(x - 2) ----> Multiplica os dois membros por -6
-6*(y + 3) = 1*(x - 2) -----> - 6y - 18 = x - 2 -----> x + 6y + 16 = 0
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por patyribeiro » Qui Set 03, 2009 13:05
por patyribeiro » Qui Set 03, 2009 13:05
Numa PA de termos positivos o 1°, o 5° eo 21° termo formam, nessa ordem, uma PG. A razão drssa PG é:
a)2
b)4
c)16
d)20
e) impossível de ser determinado.
A resposta tem que ser a letra b. Mas, por quê? Não entendi.
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por patyribeiro » Qui Set 03, 2009 13:07
por patyribeiro » Qui Set 03, 2009 13:07
Numa PG estritamente decrescente, sabe-se que a1 + a10 = -513 e a4.a7 = 512. Determine a razão dessa PG.
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por patyribeiro » Qui Set 03, 2009 13:08
por patyribeiro » Qui Set 03, 2009 13:08
Adicionando-se a mesma constante a cada um dos números 6,10 e 15 nessa ordem, obtemos uma p.g de razão:
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por patyribeiro » Qui Set 03, 2009 13:19
por patyribeiro » Qui Set 03, 2009 13:19
Uma PG tem primeiro termo igual a 1 e a razão igual a raiz quadrada de 2. Se o produto dos termos dessa progressão é 2^39, então o números de termos é igual a:
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por patyribeiro » Qui Set 03, 2009 13:21
por patyribeiro » Qui Set 03, 2009 13:21
Uma PG de 8 termos tem primeiro termo igual a 10. O logaritmo decimal do produto de seus termos vale 36. Ache a razão dessa progressão.
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por patyribeiro » Qui Set 03, 2009 13:23
por patyribeiro » Qui Set 03, 2009 13:23
O número de ancestrais de uma pessoa, em seis gerações é:
a)63
b)126
c)127
d)32
e)64
-
patyribeiro
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Set 03, 2009 12:30
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Qui Set 03, 2009 17:02
por Elcioschin » Qui Set 03, 2009 17:02
Paty
1) Por favor, não utilize um tópico aberto por outra pessoa, para postar suas dúvidas.
2) Quando tiver UMA dúvida abra um novo tópico.
3) Poste APENAS uma dúvida por tópico, seguindo as regras do forum.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem pode me ajudar com este exercício?
por phvicari » Sáb Fev 18, 2012 16:19
- 2 Respostas
- 1579 Exibições
- Última mensagem por phvicari

Sáb Fev 18, 2012 23:12
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Alguém pode me ajudar com este exercicio
por carvalhothg » Dom Set 04, 2011 18:40
- 1 Respostas
- 1754 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 20:19
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode me ajudar neste exercício, por favor...
por caducustodio » Sex Ago 17, 2012 09:00
- 1 Respostas
- 1813 Exibições
- Última mensagem por Cleyson007

Sex Ago 17, 2012 09:50
Sistemas de Equações
-
- Alguem poderia me ajudar com esse exercicio ?
por rodrigo321 » Dom Dez 06, 2009 03:33
- 1 Respostas
- 2011 Exibições
- Última mensagem por Molina

Dom Dez 06, 2009 12:09
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2542 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 sendo
sendo  o seu lado.
o seu lado.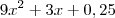 pode ser fatorado como
pode ser fatorado como 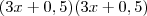 e portanto o lado do quadrado será
e portanto o lado do quadrado será 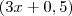
 então
então