 por Brenitchow » Qua Jun 20, 2012 17:25
por Brenitchow » Qua Jun 20, 2012 17:25
Poderia me ajudar a resolver este exercício?
Dadas estas equações, determine a soma e o produto das raízes em cada uma delas:
a) 3x² + 8x - 7 = 0
b) 2m² - 5m + 2 = 0
c) -x² - x - 20 = 0
d) 5k² + 30k = 0
-3y² + 10 = 0
Quero dicas para resolver apenas.
-
Brenitchow
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 13, 2012 19:41
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Qua Jun 20, 2012 20:47
por MarceloFantini » Qua Jun 20, 2012 20:47
Use as relações de Girard: as raízes de um polinômio
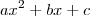
satisfazem
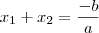
e
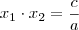
. Use isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida equação do 1 grau
por tadeutato » Qua Abr 27, 2011 14:24
- 1 Respostas
- 1436 Exibições
- Última mensagem por Neperiano

Qua Abr 27, 2011 14:29
Cálculo: Limites, Derivadas e Integrais
-
- Equação de 1º grau - dúvida
por laura_biscaro » Seg Mar 18, 2013 15:39
- 2 Respostas
- 4718 Exibições
- Última mensagem por laura_biscaro

Seg Mar 18, 2013 16:54
Equações
-
- Problemas equação 1° grau, dúvida.
por Clairelz12 » Sáb Ago 29, 2009 03:44
- 4 Respostas
- 7451 Exibições
- Última mensagem por Elcioschin

Sáb Ago 29, 2009 19:18
Álgebra Elementar
-
- [Equação 1º Grau] - Dúvida na resolução
por FernandoBasso » Qua Set 21, 2011 08:54
- 1 Respostas
- 1617 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 16:13
Álgebra Elementar
-
- Equação do segundo grau dúvida
por LuizCarlos » Qui Mai 10, 2012 20:21
- 1 Respostas
- 1303 Exibições
- Última mensagem por LuizCarlos

Qui Mai 10, 2012 23:02
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


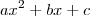 satisfazem
satisfazem 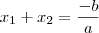 e
e 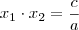 . Use isso.
. Use isso.


 .
.
 :
: