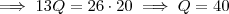por DELTAPI » Sex Set 16, 2011 14:56
por DELTAPI » Sex Set 16, 2011 14:56
Alguem poderia me auxiliar a montar este sistema de equações:
Joana foi à feira levando certa quantia em dinheiro. Na 1.ª banca, comprou legumes e gastou 1/4 dessa quantia. Na 2.ª banca, comprou verduras e gastou 2/5 do valor gasto na 1.ª banca. Na 3.ª banca, comprou frutas e gastou R$ 15,50. Sabendo-se que da quantia inicial restaram R$ 10,50, conclui-se que na compra de verduras ela gastou?
x= valor de dinheiro qeu levou
1ª Banca = x-(1/4x)
2ª Banca = 2/5 (x -1/4x)
3ª banca = R$15,50
sobrou RS10,50
Montei a equação da seguinte forma mas não deu o resultado proposto: alguem pode indicar onde eu errei?
x-(1/4x)-2/5(x-1/4)-15,50=10,50
-
DELTAPI
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 06, 2011 08:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Neperiano » Sex Set 16, 2011 15:25
por Neperiano » Sex Set 16, 2011 15:25
Ola
Transforme esse 1/4 em 0,25
Logo na 1 banca gastou 0,25
Na 2 banca gastou 2/5 de 0,25 que é 0,1 (só fazer 0,25 vezes 2 e dividido por 5)
Na 3 banca gastou 15,50
Sobrou 10,50 de tudo entao
Ela tinha 15,50+10,50=26 reais mais 0,35
Então
26 - 1
x - 0,35
Logo 9,1
Então ela tinha 26+9,1= 35,1 reais
Acho que é isso
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DELTAPI » Sáb Set 17, 2011 10:12
por DELTAPI » Sáb Set 17, 2011 10:12
PESSOAL, MUITO OBRIGADO.
NA SEGUNDA BANCA ELE GASTOU R$4,00 ( Q/10 =>R$4,00).
CASO CONHEÇAM ALGUM LIVRO QUE ENSINA COMO MONTAR AS EQUAÇÕES, FAVOR ME INDICAR.
-
DELTAPI
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Set 06, 2011 08:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4491 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- [Equações] dúvidas
por DELTAPI » Ter Set 06, 2011 08:38
- 4 Respostas
- 2097 Exibições
- Última mensagem por DELTAPI

Sex Set 09, 2011 08:36
Sistemas de Equações
-
- [Equações Diferenciais Ordinárias e Aplicações]Duvidas
por pdss » Qua Dez 07, 2011 17:56
- 1 Respostas
- 2009 Exibições
- Última mensagem por LuizAquino

Qua Dez 07, 2011 20:14
Cálculo: Limites, Derivadas e Integrais
-
- Duvidas sobre equações pares e impares
por Ricley » Qui Nov 02, 2017 00:13
- 0 Respostas
- 5135 Exibições
- Última mensagem por Ricley

Qui Nov 02, 2017 00:13
Cálculo: Limites, Derivadas e Integrais
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5533 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ; depois, gastou dois quintos do que gastou primeiro, logo
; depois, gastou dois quintos do que gastou primeiro, logo  ; por último, gastou 15,50 e sobrou 10,50. Equacionando:
; por último, gastou 15,50 e sobrou 10,50. Equacionando: