1. Um nutricionista está preparando uma refeição com 2 alimentos A e B. Cadas grama do alimenta A contém 2 unidades de próteina, 3 unidades de carbroidato e 2 unidades de gordura. Cada grama do alimento B contém 4 unidades de Carbroidato 4 unidades de próteina e 3 unidades de gordura,. Essa refeição devera fornecer exatamente 400 unidades de proteinas e 500 unidades de carbroidatos.
A quantidade de gordura que esta refeição ira fornecer e?
2. André, Bento e Carlos têm, juntos, 41 anos. Sabe-se que Bento e 3 anos mias velho que André e Carlos 4 anos mias jovem que André. Se as idade de, André Bento e Carlos são respectivamente, a, b e c, então o valor de 2a-b-c é?
Meu problema e que eu não sei montar as equações, então se vcs puderem monta-las pra mim e explicar como fizeram eu agradeço.



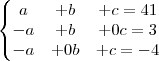

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)