 por Claudin » Sáb Mar 17, 2012 10:42
por Claudin » Sáb Mar 17, 2012 10:42
Gostaria de saber técnicas para escalonamento de sistemas lineares que não são "quadrados", por exemplo de ordem 4x4, 3x3...
Em sistemas 3x3, 4x4, 5x5, 6x6 consigo escalonar normalmente pelo método de Gauss Jordan.
Agora minha dúvida persiste em sistemas como estes abaixo:
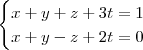
Outra dúvida seria nesse sistema também:
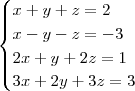
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Mar 17, 2012 15:23
por MarceloFantini » Sáb Mar 17, 2012 15:23
Quando o sistema tem mais incógnitas que equações, ele não tem solução única. O método de escalonamento é o mesmo, só que você vai deixar algumas em função de outras. Neste caso, como você tem 2 equações e 4 incógnitas, terá 2 incógnitas em função das outras duas. No caso geral, com

equações e

incógnitas, com
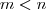
, então terá

incógnitas em função de

. Quando temos mais equações que incógnitas, isto significa que uma ou mais são combinações das outras, ou seja, podemos descartá-las pois elas não interferem na solução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Sáb Mar 17, 2012 15:47
por Claudin » Sáb Mar 17, 2012 15:47
Continuo com resultados errados, em relação a resposta do exercício.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Mar 17, 2012 15:51
por MarceloFantini » Sáb Mar 17, 2012 15:51
Mostre o seu desenvolvimento.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Sáb Mar 17, 2012 16:15
por Claudin » Sáb Mar 17, 2012 16:15
O 1º exemplo que relatei obtive como resultado:
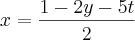
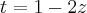
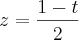
O segundo exemplo está impossível de postar o desenvolvimento todo, pois esqueci os códigos da matriz no latex, e o desenvolvimento ficou confuso, grande e errado, então irei postar a resposta logo abaixo.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Sáb Mar 17, 2012 16:17
por Claudin » Sáb Mar 17, 2012 16:17
O 2º exemplo que postei acima encontrei como resposta o seguinte:
1 0 0 -3
0 1 0 -1
0 0 0 0
0 0 1 -1
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Mar 17, 2012 16:31
por MarceloFantini » Sáb Mar 17, 2012 16:31
No primeiro

. Substituindo na outra, teremos
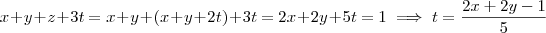
.
Voltando em z, segue
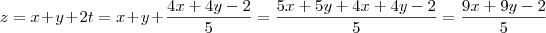
. Pronto, temos duas incógnitas em termos das outras duas.
Se o seu desenvolvimento da segunda estiver certo, então segue que

,
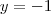
e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Dom Mar 18, 2012 11:39
por Claudin » Dom Mar 18, 2012 11:39
continuo sem entender sobre a 2ª questão, pois a resposta está incorreta
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7151 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3568 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6722 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4692 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4802 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
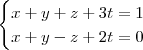
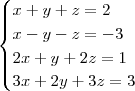

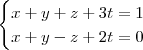
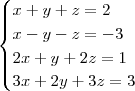

 equações e
equações e  incógnitas, com
incógnitas, com 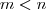 , então terá
, então terá  incógnitas em função de
incógnitas em função de  . Quando temos mais equações que incógnitas, isto significa que uma ou mais são combinações das outras, ou seja, podemos descartá-las pois elas não interferem na solução.
. Quando temos mais equações que incógnitas, isto significa que uma ou mais são combinações das outras, ou seja, podemos descartá-las pois elas não interferem na solução.



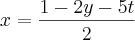
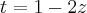
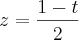


 . Substituindo na outra, teremos
. Substituindo na outra, teremos 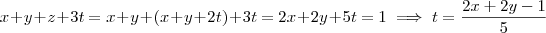 .
. 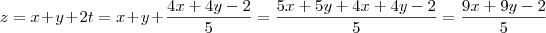 . Pronto, temos duas incógnitas em termos das outras duas.
. Pronto, temos duas incógnitas em termos das outras duas. ,
, 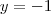 e
e  .
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
