Bom, eu aaacho que o que voce quis dizer foi


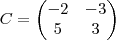
Basicamente, o que se deve fazer é...
se voce precisa somar (ou subtrair) duas matrizes. voce soma (ou subtração) termo por termo, respectivamente.
Por exemplo

Se voce quiser multiplicar por um escalar... tipo 2, voce multiplica todos os membros por 2. (o mesmo vale para divisão por escalar)
Agora o mais chatinho. Se voce precisa Multiplicar duas matrizes, voce vai ter que:
Somar a multiplicação respectiva de uma linha da matriz da esquerda, com uma linha da matriz da direita. o melhor jeito de aprender isso é com exemplos.
Usando a letra a) como exemplo.
calcule antes de qualquer coisa 2A e 2B
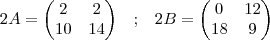
agora multipliquemos...
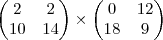
Voce deve fazer o seguinte.
pegue a
PRIMEIRA linha da matriz da esquerda, e a
PRIMEIRA coluna da matriz da direita.
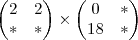
Multiplique o termo A11 com o B11, e some com A21 vezes o termo B12.
assim:
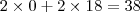
Esse numero ficará no lugar de coordenadas 1,1 da resposta, pois voce pegou a PRIMEIRA linha e a PRIMEIRA coluna...
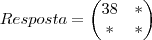
Depois vamos pegar a PRIMEIRA linha e a SEGUNDA coluna
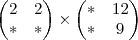
A11 vezes B21, mais, A12 vezes B22... {Um bom jeito de fazer essa multiplicação de forma automática é não pensar nesses numeros! coloque o dedo no começo de uma linha e outro dedo no começo de uma coluna... Vá andando os dedos e multiplicando termo à termo! Uma dica... eu GARANTO que se voce fizer 5 multiplicações de matriz por 3 dias seguidos (isso da uns 10 minutos) voce vai fazer essa multiplicação automática... eu digo isso pq confunde, essa multiplicação é chata!}
vai resultar em 36 essa ultima

... e voce vai posicioná-la no termo de coordenadas 1,2 da resposta, por que usou a PRIMEIRA linha com a SEGUNDA coluna. resultando
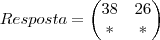
depois voce precisa fazer da SEGUNDA linha com a PRIMEiRA coluna
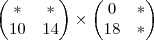

e vai resultar 252
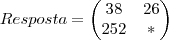
tente fazer a ultima sosinho.
--> quando voce precisar calcular uma transposta... ou
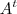
só o que se deve fazer é inverter as linhas pelas colunas.
--> Quando voce precisar de uma matriz inversa, ou
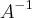
Voce deve multiplicar a matriz A por uma matriz desconhecida... ou seja,
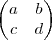
e tomar como resultado a matriz identidade

isso vai resultar num sistema facil de ser resolvido.
.
{{ Eu realmente espero que tenha ajudado! demorei quase uma hora pra responder esse topico! AUSHASUHAHUSAHU }}
bom estudo
.




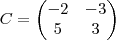

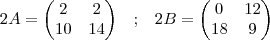
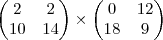
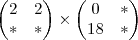
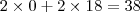
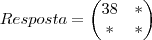
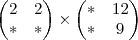
 ... e voce vai posicioná-la no termo de coordenadas 1,2 da resposta, por que usou a PRIMEIRA linha com a SEGUNDA coluna. resultando
... e voce vai posicioná-la no termo de coordenadas 1,2 da resposta, por que usou a PRIMEIRA linha com a SEGUNDA coluna. resultando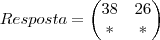
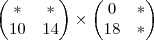

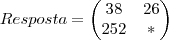
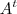
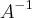 Voce deve multiplicar a matriz A por uma matriz desconhecida... ou seja,
Voce deve multiplicar a matriz A por uma matriz desconhecida... ou seja,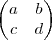


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.