Olá Manoella e Renato_RJ,
O colega Renato_RJ equivocou-se, pois os vetores (2,1) e (1,1) formam sim uma base para

. Note que a equação

tem como
única solução

, significando portanto que os vetores são L.I. Mas, dois vetores L.I. no espaço vetorial

sempre formam uma base para o mesmo.
Sendo assim, primeiro vamos escrever um vetor (x,y) qualquer em função dos vetores da base. Ou seja, vamos resolver a equação (nas incógnitas k e m):
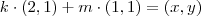
De onde obtemos o sistema:
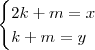
A solução desse sistema é:
k=x-y e
m=2y-x. Portanto, podemos escrever qualquer vetor (x,y) em função da base da seguinte forma:
(x, y) = (x-y)(2, 1) + (2y-x)(1, 1)
Considerando que
T é transformação linear, podemos fazer:
T(x, y) = T((x-y)(2, 1) + (2y-x)(1, 1))
T(x, y) = (x-y)T(2, 1) + (2y-x)T(1, 1)
Substituindo T(2, 1) e T(1, 1) dados:
T(x, y) = (x-y)(1, 2, 0) + (2y-x)(0, -3, 5)
Fazendo as contas, obtemos:
T(x, y)=(x-y, 5x-8y, -5x+10y)
Para conferir a resposta, basta você calcular T(2, 1) e T(1, 1):
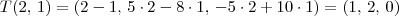
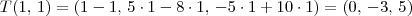
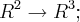 tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)
tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)
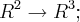 tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)
tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)

 . Note que a equação
. Note que a equação
 , significando portanto que os vetores são L.I. Mas, dois vetores L.I. no espaço vetorial
, significando portanto que os vetores são L.I. Mas, dois vetores L.I. no espaço vetorial  sempre formam uma base para o mesmo.
sempre formam uma base para o mesmo.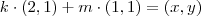
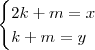
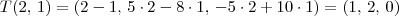
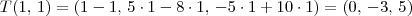


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)