T:
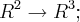 tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)
tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)Como faço para descobrir a lei de definição de T?

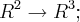 tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)
tal que T(2,1)= (1,2,0) e T (1,1)=(0,-3,5)

 . Note que a equação
. Note que a equação
 , significando portanto que os vetores são L.I. Mas, dois vetores L.I. no espaço vetorial
, significando portanto que os vetores são L.I. Mas, dois vetores L.I. no espaço vetorial  sempre formam uma base para o mesmo.
sempre formam uma base para o mesmo.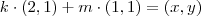
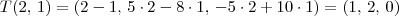
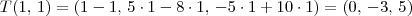


Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.