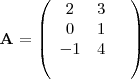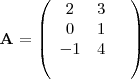por Felicia » Ter Set 15, 2009 00:11
por Felicia » Ter Set 15, 2009 00:11
Preciso fazer uma soma com duas matrizes porém de tipos diferentes. 2x3 + 3x2, a minha dúvida para efetuar essa soma, somente será possível se transformar em transposta, estou correta?
[ 2 3 ]
A = [ 0 1 ] e B= [1 2 3 ]
[ -1 4] [-2 0 4]
- A+B
- A-B
- 2(A+B)
- Axb
Este é o exercício como posso fazer a adição se só posso adicionar se forem matrizes de mesmo tipo?
Agradeço a atenção,
Felicia

-
Felicia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Set 14, 2009 23:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Elcioschin » Ter Set 15, 2009 09:19
por Elcioschin » Ter Set 15, 2009 09:19
Felícia
Duas matrizes podem ser somadas SOMENTE se forem da MESMA ordem m*n.
Assim, no teu exercício a função SOMA não existe.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CÁLCULO DE LIMITE COM RAIZES DE ÍNDICES DIFERENTES
por thiago15_2 » Qui Fev 27, 2014 01:20
- 1 Respostas
- 2427 Exibições
- Última mensagem por young_jedi

Sex Fev 28, 2014 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Probabilidade Alunos e tipos música
 por Lana Brasil » Qua Abr 17, 2013 18:54
por Lana Brasil » Qua Abr 17, 2013 18:54
- 8 Respostas
- 6802 Exibições
- Última mensagem por Lana Brasil

Sáb Abr 27, 2013 15:34
Probabilidade
-
- Alguem me passa esses tipos de exercícios?
por gomusalie » Qui Out 27, 2011 19:47
- 0 Respostas
- 1056 Exibições
- Última mensagem por gomusalie

Qui Out 27, 2011 19:47
Funções
-
- Alguem me passa esses tipos de exercícios?
por gomusalie » Qui Out 27, 2011 19:47
- 0 Respostas
- 1063 Exibições
- Última mensagem por gomusalie

Qui Out 27, 2011 19:47
Funções
-
- [Tipos especiais de operadores lineares] Cap. 9 Boldrini
por santossilvaane » Sáb Mar 26, 2016 18:00
- 1 Respostas
- 1948 Exibições
- Última mensagem por adauto martins

Dom Mar 27, 2016 11:20
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.