 por GABRIELA » Ter Set 08, 2009 21:41
por GABRIELA » Ter Set 08, 2009 21:41
Estou com a seguinte questão de sistema:
2x-y = 7
x+4y=-1Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkk

Tentei!!!
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Set 09, 2009 00:18
por Molina » Qua Set 09, 2009 00:18
GABRIELA escreveu:Estou com a seguinte questão de sistema:
2x-y = 7
x+4y=-1Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkk

Tentei!!!
Boa noite, Gabriela.
Em sistemas lineares os mesmo valores de
x e
y encontrados tem que satisfazer ambas equações.
Um dos modos mais fáceis e usados para resolver isso é isolar uma incognita (x ou y) em uma das equações e substituir o valor correspondente na outra equação, ficando assim com apenas uma variável. Assim:

(equação 1)
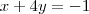
(equação 2)
1) Isole o x da
equação 2, ou seja, deixa x sozinho de um lado do igual e o restante do outro lado.
2) Na
equação 1 subtitua o x que está junto com o

pelo valor encontrado no item 1).
3) Com isso você vai ficar apenas com y na equação, sendo possível determinar o valor dele.
4) Com o valor de y achado, substitua em qualquer uma das equações e encontre o valor de x.
Tente e comente qualquer novidade.
Até mais.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Qua Set 09, 2009 17:10
por GABRIELA » Qua Set 09, 2009 17:10
molina escreveu:GABRIELA escreveu:Estou com a seguinte questão de sistema:
2x-y = 7
x+4y=-1Então fiz assim
8x-4y=7
4x=7
x=7-4
x=3
Não entendo muito como resolve sistema então fiz assim,mas não estou sabendo resolver para achar o outro valor.
Se estiver errado fazer assim,pelo menos achei o valor de um deles.kkkkk

Tentei!!!
Boa noite, Gabriela.
Em sistemas lineares os mesmo valores de
x e
y encontrados tem que satisfazer ambas equações.
Um dos modos mais fáceis e usados para resolver isso é isolar uma incognita (x ou y) em uma das equações e substituir o valor correspondente na outra equação, ficando assim com apenas uma variável. Assim:

(equação 1)
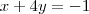
(equação 2)
1) Isole o x da
equação 2, ou seja, deixa x sozinho de um lado do igual e o restante do outro lado.
2) Na
equação 1 subtitua o x que está junto com o

pelo valor encontrado no item 1).
3) Com isso você vai ficar apenas com y na equação, sendo possível determinar o valor dele.
4) Com o valor de y achado, substitua em qualquer uma das equações e encontre o valor de x.
Tente e comente qualquer novidade.
Até mais.

Blz!Fiz como vc me ensinou achei 3 e 1,só que deve ser -1  Ahh1 Sou péssima em resolver sistema...
Ahh1 Sou péssima em resolver sistema...
Me ajuda resolver?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Set 09, 2009 17:41
por Molina » Qua Set 09, 2009 17:41
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Qua Set 09, 2009 18:05
por GABRIELA » Qua Set 09, 2009 18:05
Ok! Entendi como resolve um sistema desse.
Obrigada!
Mas agora eu tenho um sistema que tem 3 equações.
Veja:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
O procedimento não vai ser o mesmo da anterior,vai?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Set 09, 2009 18:39
por Molina » Qua Set 09, 2009 18:39
GABRIELA escreveu:Ok! Entendi como resolve um sistema desse.
Obrigada!
Mas agora eu tenho um sistema que tem 3 equações.
Veja:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
O procedimento não vai ser o mesmo da anterior,vai?
Olá, Gabriela.
Para perguntas diferentes, tópicos diferentes, ok? Então nas próximas crie um novo tópico. Mas essa vou responder aqui:
O procedimento é diferente do anterior. Durante seus estudos você vai ver diferentes maneiras de encontrar a mesma coisa (no caso, de encontrar
x,
y e
z).
Por agora, não posso lhe ajudar, pois não sei qual ferramentas você ja viu nas aulas. Escalonamento? Cramer?
Aproveito aqui já para corrigir seu erro de digitação:
GABRIELA escreveu:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
Correto:
(mudei aqui!)



Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Qua Set 09, 2009 18:52
por GABRIELA » Qua Set 09, 2009 18:52
molina escreveu:GABRIELA escreveu:Ok! Entendi como resolve um sistema desse.
Obrigada!
Mas agora eu tenho um sistema que tem 3 equações.
Veja:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
O procedimento não vai ser o mesmo da anterior,vai?
Olá, Gabriela.
Para perguntas diferentes, tópicos diferentes, ok? Então nas próximas crie um novo tópico. Mas essa vou responder aqui:
O procedimento é diferente do anterior. Durante seus estudos você vai ver diferentes maneiras de encontrar a mesma coisa (no caso, de encontrar
x,
y e
z).
Por agora, não posso lhe ajudar, pois não sei qual ferramentas você ja viu nas aulas. Escalonamento? Cramer?
Aproveito aqui já para corrigir seu erro de digitação:
GABRIELA escreveu:
x + x + z = -1
2x - y - 3z = 5
x + 2y + z = 0
Correto:
(mudei aqui!)



ok! Então vou abrir um novo tópico com a mesma pergunta.
Na verdade eu ja vi toda essa matéria, estou fazendo uma revisão de algumas coisas, só que sistema não me lembro muito.
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas
por Jansen » Dom Mai 10, 2009 00:01
- 5 Respostas
- 4690 Exibições
- Última mensagem por Molina

Seg Mai 11, 2009 04:36
Sistemas de Equações
-
- sistemas
por Magda » Sex Jun 19, 2009 18:37
- 5 Respostas
- 3726 Exibições
- Última mensagem por Magda

Sex Ago 07, 2009 19:49
Sistemas de Equações
-
- Sistemas
por GABRIELA » Qua Set 09, 2009 18:59
- 2 Respostas
- 1711 Exibições
- Última mensagem por GABRIELA

Qui Set 10, 2009 17:08
Sistemas de Equações
-
- Sistemas
por GABRIELA » Seg Set 21, 2009 17:25
- 4 Respostas
- 2390 Exibições
- Última mensagem por GABRIELA

Ter Set 22, 2009 09:45
Sistemas de Equações
-
- Sistemas
por Douglaspimentel » Qui Abr 15, 2010 18:39
- 1 Respostas
- 2415 Exibições
- Última mensagem por Elcioschin

Qui Abr 15, 2010 20:14
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


Tentei!!!
 (equação 1)
(equação 1)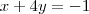 (equação 2)
(equação 2) pelo valor encontrado no item 1).
pelo valor encontrado no item 1).

Tentei!!!
(equação 1)
(equação 2)
pelo valor encontrado no item 1).


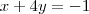

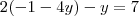
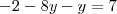
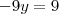
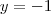





 (mudei aqui!)
(mudei aqui!)



(mudei aqui!)
