 por anneliesero » Ter Out 16, 2012 15:26
por anneliesero » Ter Out 16, 2012 15:26
Podem me ajudar? A alternativa certa é a letra C. Mas, por quê? Quais foram os erros das outras alternativas para que elas pudessem estar certas?
(PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . C
b) (A + B)t = At + Bt
c) (A . B)t = At . Bt
d) (A - B)C = AC - BC
e) (At)t = A
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Out 16, 2012 19:07
por MarceloFantini » Ter Out 16, 2012 19:07
Quais foram os erros das outras alternativas para que elas pudessem estar certas?
Você quer dizer qual o erro da alternativa C para que ela seja resposta.
O correto é
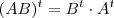
. Você pode verificar calculando os dois lados, mas uma outra forma é perceber que um elemento do produto será da forma
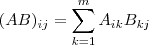
. Ao realizar uma transposição, você troca os índices da linha e coluna, basta rearranjar para ver que é igual.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7153 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3569 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6723 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4695 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4802 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


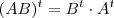 . Você pode verificar calculando os dois lados, mas uma outra forma é perceber que um elemento do produto será da forma
. Você pode verificar calculando os dois lados, mas uma outra forma é perceber que um elemento do produto será da forma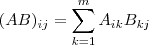 . Ao realizar uma transposição, você troca os índices da linha e coluna, basta rearranjar para ver que é igual.
. Ao realizar uma transposição, você troca os índices da linha e coluna, basta rearranjar para ver que é igual.



 , avisa que eu resolvo.
, avisa que eu resolvo.

