 por monicadiasf » Ter Abr 24, 2012 00:37
por monicadiasf » Ter Abr 24, 2012 00:37
Olá pessoas! Sou novata por aqui.. Encontrei o site quando procurava pela resolução de alguns exercícios de matemática, além das teorias disponíveis no fórum. Espero poder ajudar sempre que possível! Minha primeira dúvida envolve o seguinte exercício:
(EsPCEx) - Considere a matriz quadrada A =
![\[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\] \[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\]](/latexrender/pictures/9232a4bc5bf23b6635ec4d8f76334836.png)
.
O valor do determinante de A é:
a) -2
b) -1
c) 0
d) 1
e) 2
Letra C (queria colocar oculto, mas não sei fazer isso xD)
obs1.: Não sei porque o  saiu na minha fórmula em formato Latex (ainda estou aprendendo como isso funciona). Acho que deu para entender que se trata de ângulos, né?
obs2.: Eu comecei a resolução tentando encontrar o determinante pela Regra de Sarrus e pensei em transformar todos os elementos em sen ou cos de 18º através das fórmulas:
cos(a + b) = cos a · cos b - sen a · sen b
sen(a + b) = sen a · cos b + sen b · cos a
Pois:
36º = 18º + 18º
54º = 18º + 36º
72º = 18º + 54º
Mas ficou muito grande e eu acabei me perdendo!

Ajuda??
Muuuito obrigada!
-
monicadiasf
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 20, 2012 15:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisioterapia
- Andamento: cursando
 por Russman » Ter Abr 24, 2012 04:18
por Russman » Ter Abr 24, 2012 04:18
Veja que esta matriz é quadrada, de ordem 2. Assim, seu determinante é diferença do produto dos elementos das diagonais princiapal e secundária.
Isto é:

Agora observe que
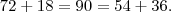
.
Assim,
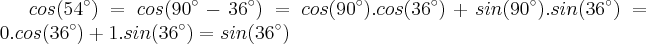
e
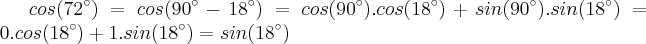
Portanto,
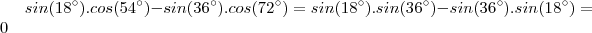
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX)Função
por natanskt » Sex Out 15, 2010 23:48
- 1 Respostas
- 1749 Exibições
- Última mensagem por DanielRJ

Sáb Out 16, 2010 00:30
Funções
-
- (ESPCEX)Função
por natanskt » Ter Out 19, 2010 10:20
- 2 Respostas
- 3852 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 17:42
Funções
-
- (ESPCEX)Função
por natanskt » Ter Out 19, 2010 10:38
- 2 Respostas
- 4198 Exibições
- Última mensagem por natanskt

Qua Out 20, 2010 10:05
Funções
-
- (ESPCEX)Função
por natanskt » Ter Out 19, 2010 10:47
- 1 Respostas
- 3324 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 17:32
Funções
-
- (ESPCEX)Função
por natanskt » Ter Out 19, 2010 10:52
- 1 Respostas
- 2647 Exibições
- Última mensagem por DanielRJ

Ter Out 19, 2010 16:10
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\] \[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\]](/latexrender/pictures/9232a4bc5bf23b6635ec4d8f76334836.png) .
. 



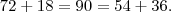 .
.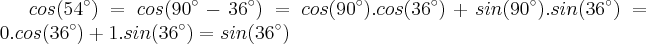
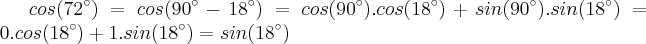
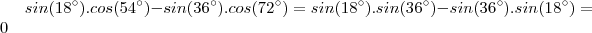

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.