(EsPCEx) - Considere a matriz quadrada A =
![\[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\] \[
\left(
\begin{array}{ccc}
sen18º & cos72º \\
sen36º & cos54º \end{array}
\right)\]](/latexrender/pictures/9232a4bc5bf23b6635ec4d8f76334836.png) .
. O valor do determinante de A é:
a) -2
b) -1
c) 0
d) 1
e) 2
Letra C (queria colocar oculto, mas não sei fazer isso xD)
obs1.: Não sei porque o  saiu na minha fórmula em formato Latex (ainda estou aprendendo como isso funciona). Acho que deu para entender que se trata de ângulos, né?
obs2.: Eu comecei a resolução tentando encontrar o determinante pela Regra de Sarrus e pensei em transformar todos os elementos em sen ou cos de 18º através das fórmulas:
cos(a + b) = cos a · cos b - sen a · sen b
sen(a + b) = sen a · cos b + sen b · cos a
Pois:
36º = 18º + 18º
54º = 18º + 36º
72º = 18º + 54º
Mas ficou muito grande e eu acabei me perdendo!

Ajuda??
Muuuito obrigada!



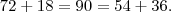 .
.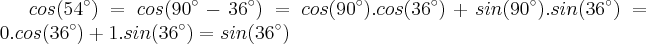
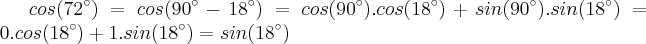
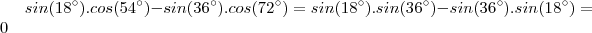


 .
.
 :
: