diogenesos escreveu:(UFRN RN) A solução da equação matricial
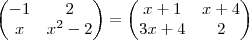
é um numero:
diogenesos escreveu:Não faço ideia de como solucionar a equação, na verdade eu sei o resultado, mas não sei chegar nele.
Para que duas matrizes sejam iguais, todos os seus elementos em posições correspondentes devem ser iguais.
Por exemplo, se A = B, então o elemento

de A é igual ao elemento

de B . De modo geral, se A = B, então o elemento

de A deve ser igual ao elemento
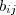
de B.
No caso do exercício, comparando os elementos temos as seguintes equações:
-1 = x + 1
2 = x + 4
x = 3x + 4
x² - 2 = 2
Você deve obter um mesmo valor para x que resolva todas essas equações. Se isso acontecer, então as matrizes serão iguais. Ou seja, a equação matricial terá solução.
Agora tente terminar o exercício.



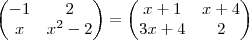
 de A é igual ao elemento
de A é igual ao elemento  de B . De modo geral, se A = B, então o elemento
de B . De modo geral, se A = B, então o elemento  de A deve ser igual ao elemento
de A deve ser igual ao elemento 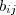 de B.
de B.


 , avisa que eu resolvo.
, avisa que eu resolvo.

