Olá pessoal, poderiam me ajudar na questão a seguir:
Dados os vetores u=(1, a, -2a-1), v=(a,a-1,1) e w=(a,-1,1), determinar "a" de modo que u.v=(u+v)w.
Cheguei a conclusão que a=2 fazendo o seguinte:
u.v=(1,a,-2a-1)(a,a-1,1)=a²-2a-1
u+v=(1+a,2a-1,-2a)
(u+v)w=a²-3a+1
u.v=(u+v)w
a²-2a-1=a²-3a+1
a=2







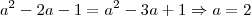

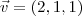

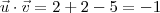




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)