 por luix henrique » Seg Out 13, 2008 15:42
por luix henrique » Seg Out 13, 2008 15:42
poderiam me ajuda nesses exercicios que ja tentei de toda forma mas noa consegui resolve-los
é sobre matrizes
1-represente explicitamente cada uma das matrizes:
a)A=(aij)2x2 tal que aij=(-1)elevado i+j:
b)A=(aij)3x2 tal que aij={0 se i=j }:
{2i+j se i>j}
{j se i<j}
2-sao dadas as matrizesA=(3),B=(4) e C=(-2).resolva a equaçao "x+2.A(elevado a '' t'')=3.(B+C)(elevado a '' t''):
(2) (1) (1)
3-determine,se existir,a inversa da matriz (2 3)
(4 5):
é a ultima q é a pior de todas nao consegui de nenhum geito fazer
4-se ''A'' e "B" sao matrizes tais que A=(2 1) e B=(1 1 )calcule a matriz y=A(elevado a '' t'') .B:
(1 0) (2 5 )
(-3 1) (0 -1)
Editado pela última vez por
luix henrique em Ter Out 14, 2008 13:01, em um total de 1 vez.
-
luix henrique
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Out 13, 2008 15:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Out 13, 2008 20:13
por Molina » Seg Out 13, 2008 20:13
Boa tarde, Luix Henrique.
Procure se informar como se escreve no forum através do LaTeX, onde a formatação das matrizes ficam certinhas e isso facilita a visualização de quem quer te ajudar.
luix henrique escreveu:1-represente explicitamente cada uma das matrizes:
a)A=(aij)2x2 tal que aij=(-1)elevado i+j:
Vou te ajudar nessa.
Vamos ver se tu consegue fazer as outras então:
a)
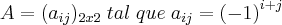
Com isso temos uma matriz de ordem 2x2, ou seja, 2 linhas e 2 colunas:
![A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\]](/latexrender/pictures/66b8e25dbcade0416c564aa835461b68.png)
 IMPORTANTE: O
IMPORTANTE: O  é o numero da linha e o
é o numero da linha e o 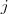 é o numero da coluna:
é o numero da coluna:![A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\]](/latexrender/pictures/a83cd364e4d481ed2da78444b50e8b49.png)
Utilizando o enunciado
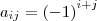
:

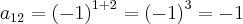
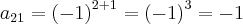

Logo:
![A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\]](/latexrender/pictures/8217b310ddf354499e103a193b8da902.png)

Bom estudo!
Se nao conseguir fazer as outras é só avisar.
Abraços!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5151 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3593 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 5996 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12789 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
-
- Matrizes
por Cleyson007 » Sáb Nov 01, 2008 00:51
- 2 Respostas
- 3038 Exibições
- Última mensagem por Cleyson007

Sex Mai 29, 2009 11:14
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


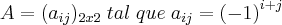
![A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{ij} & {a}_{ij} \\
{a}_{ij} & {a}_{ij} \end{array}
\right)\]](/latexrender/pictures/66b8e25dbcade0416c564aa835461b68.png)
 IMPORTANTE: O
IMPORTANTE: O  é o numero da linha e o
é o numero da linha e o 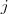 é o numero da coluna:
é o numero da coluna:![A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
{a}_{11} & {a}_{12} \\
{a}_{21} & {a}_{22} \end{array}
\right)\]](/latexrender/pictures/a83cd364e4d481ed2da78444b50e8b49.png)
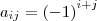 :
:
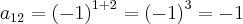
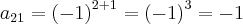

![A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\] A=\[
\left(
\begin{array}{ccc}
1 & -1 \\
-1 & 1 \end{array}
\right)\]](/latexrender/pictures/8217b310ddf354499e103a193b8da902.png)
 Bom estudo!
Bom estudo!