 por aliceit » Ter Abr 26, 2011 22:52
por aliceit » Ter Abr 26, 2011 22:52
Uma indústria de produtos natalinos encerrou o ano de 2006, com um estoque de 250 peças. Em janeiro de 2007, a indústria concedeu férias coletivas a seus funcionários e a partir de fevereiro recomeçou sua produção. Com base no texto, considerando que essa indústria, em fevereiro, produziu 550 produtos, que a cada mês essa produção cresceu em progressão aritmética e que em novembro de 2007 o estoque passou a ter 26000 itens, é correto afirmar que o número de peças produzidas em agosto foi de..?
Eu tentei a soma dos termos da P.A., juntando primeiro o 250 com o 550 (produção de fevereiro):
S10 = a1 + a10 * 10/5
26.000 = 800 + a10 * 10/5
a10 = 4400
depois eu coloquei na forma do termo geral:
a10 = a1 + 9R
4400 = 800 + 9R
R = 400
então, apliquei no termo geral para saber o mês de agosto:
a7 = a1 + 6R
a7 = 800 + 6*400
a resposta é 3250!, mas só acho 3200
por favor, me ajudem!!
-
aliceit
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 26, 2011 21:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 27, 2011 00:36
por MarceloFantini » Qua Abr 27, 2011 00:36
Você errou aqui: primeiro, novembro é

e não
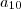
; segundo, quando você trabalha com peças produzidas, você não conta o estoque do ano 2006 - você quer
apenas as peças produzidas a cada mês, e as peças de 2006 não foram produzidas em 2007 (óbvio, sim). Refaça suas contas e chegará ao resultado certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por aliceit » Qua Abr 27, 2011 10:31
por aliceit » Qua Abr 27, 2011 10:31
olá!
obrigada por dispensar seu tempo para me ajudar.
eu tentei fazer o que você disse: novembro como a9, e desprezei o estoque de 2006.
no entanto a conta ficou muito esquisita e não cheguei ao resultado.
vou continuar tentando,
valeu!
-
aliceit
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 26, 2011 21:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 27, 2011 19:46
por MarceloFantini » Qua Abr 27, 2011 19:46
Cacete (desculpe), cometi um erro e ainda por cima tive um tremendo trabalho refazendo meus passos pra descobrir como cheguei na resposta. Aqui vai:
Primeiro, você estava certo. É
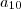
mesmo, perdão pelo erro!
Segundo, a resolução segue assim:
A soma de todos as produções JUNTAMENTE com o estoque antigo deve somar 26000, logo:

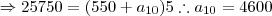
Usando a definição de termo geral de P.A.:
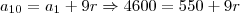

Calculando o número de peças em agosto:


Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por aliceit » Qua Abr 27, 2011 23:22
por aliceit » Qua Abr 27, 2011 23:22
Fantini,
super agradeço a sua colaboração!
hoje a noite consegui resolver a questão, e quando loguei aqui para te mostrar vi a surpresa!
digamos que a sua resolução ficou mais organizada que a minha, hauahuahua.
mais uma vez obrigada,
muita paz e muito sucesso na sua vida!
-
aliceit
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 26, 2011 21:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 27, 2011 23:30
por MarceloFantini » Qua Abr 27, 2011 23:30
É uma resolução bem explicada e resolvida, como os alunos deveriam ser ensinados no ensino médio, e não álgebras sem explicações. Fico feliz que apesar do meu erro você tenha conseguido por conta própria! Muita paz e sucesso para você também.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda com resolução do problema
por Mimizinha » Qua Mar 19, 2008 16:46
- 2 Respostas
- 2547 Exibições
- Última mensagem por Mimizinha

Qua Mar 19, 2008 17:34
Geometria Plana
-
- resolução de problema de matemática
por mauro arkader » Dom Abr 06, 2008 01:30
- 1 Respostas
- 3318 Exibições
- Última mensagem por admin

Dom Abr 06, 2008 07:44
Álgebra Elementar
-
- [Integrais] Problema com resolucao
 por gabrielnandi » Qui Jun 28, 2012 01:25
por gabrielnandi » Qui Jun 28, 2012 01:25
- 1 Respostas
- 1623 Exibições
- Última mensagem por Russman

Qui Jun 28, 2012 08:12
Cálculo: Limites, Derivadas e Integrais
-
- [Problema na resolução do logaritmo]
por Mayra Luna » Qui Out 25, 2012 20:14
- 2 Respostas
- 1512 Exibições
- Última mensagem por Mayra Luna

Qui Out 25, 2012 21:24
Logaritmos
-
- matemática- resolução de problema
por zenildo » Qui Mai 30, 2013 21:27
- 1 Respostas
- 1546 Exibições
- Última mensagem por Rafael16

Qui Mai 30, 2013 23:04
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e não
e não 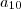 ; segundo, quando você trabalha com peças produzidas, você não conta o estoque do ano 2006 - você quer
; segundo, quando você trabalha com peças produzidas, você não conta o estoque do ano 2006 - você quer 


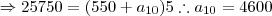
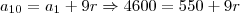



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.