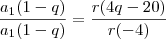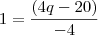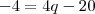por jose henrique » Qui Set 30, 2010 08:17
por jose henrique » Qui Set 30, 2010 08:17
Numa PA de termos positivos, o 1°, 5° e o 21° termo formam, nessa ordem uma pg. A razão dessa Pg é?
Eu não sei nem por onde começar está questão, tentei resolve-la com a propriedade da média geométrica mas não consegui. O que mais está me confundido é o fato de passar uma sequência pa para uma sequência PG
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Molina » Qui Set 30, 2010 18:06
por Molina » Qui Set 30, 2010 18:06
Boa tarde.
Por definição, podemos escrever o 1°, 5° e 21° termos da PA da seguinte forma, respectivamente:

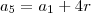

E como esses termos formam uma PG, e sabemos que se eu pegar um termo da PG e dividir pelo termo anterior, nos fornece a razão, temos as seguintes equações:
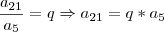
e
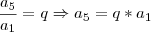
Substituindo esses valores e ajustando ela melhor, você chegará em:

e
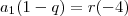
Dividindo a de cima pela de baixo:

Note aqui que o
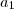
e o

irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau:
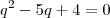
onde as raízes são 4 e 1. Como se a razão de uma PG for 1 ela é constante, ficamos com

.
Não fiz uma prova real para ve se esse é o valor correto. Então, caso você faça, poste aqui!
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por jose henrique » Qui Set 30, 2010 21:10
por jose henrique » Qui Set 30, 2010 21:10
eu não consegui entender como vc chegou nestes valores:
a1 (1+q)=r(4q-20)
e
a1(1-q)=r(-4)
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Molina » Qui Set 30, 2010 21:51
por Molina » Qui Set 30, 2010 21:51
jose henrique escreveu:eu não consegui entender como vc chegou nestes valores:
a1 (1+q)=r(4q-20)
e
a1(1-q)=r(-4)
Boa noite.
Vendo agora percebo que cometi um erro de sinal. Vou mostrar aqui a solução correta e os passos de como cheguei ao final (respondendo sua dúvida):
Usei o fato de
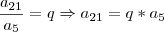
, pois:

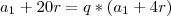
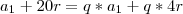

 Note que na minha primeira resolução havia trocado o sinal antes da igualdade. Ao invés de negativo havia colocado positivo, MAS O CERTO É NEGATIVO!
Note que na minha primeira resolução havia trocado o sinal antes da igualdade. Ao invés de negativo havia colocado positivo, MAS O CERTO É NEGATIVO! Desse mesmo modo você chega a partir de
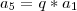
em
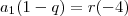
Agora fica mais fácil ainda, veja:
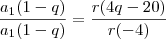
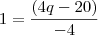
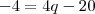


Acho que agora está certo.
Qualquer dúvida, informe!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por jose henrique » Qui Set 30, 2010 22:16
por jose henrique » Qui Set 30, 2010 22:16
ufa!, rapaz eu achei que não iria entender este tipo de questão. Obrigado!!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



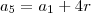

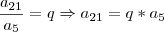
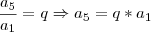

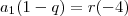

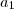 e o
e o  irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau:
irão se anular. Multiplicando cruzado cairemos numa equação do 2° grau: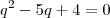
 .
.


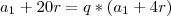
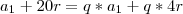


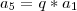 em
em