 por yanagranhen » Seg Jun 21, 2010 22:06
por yanagranhen » Seg Jun 21, 2010 22:06
(ufrs) Considere o enunciado abaixo, que descreve etapas de uma construção.Na primeira etapa,toma-se um quadrado de lado 1. Na segunda, justapoe-se um novo quadrado de lado 1 adjacente a cada lado do quadrado de lado inicial.Em cada nova etapa, justapoem-se novos quadrados de lado 1 ao longo da figura obtida na etapa anterior, como esta representado abaixo:
1ª Etapa
?
2ª Etapa
?
???
?
3ªº etapa
?
???
?????
???
?
4ª etapa
?
???
?????
???????
?????
???
?
Seguindo esse padrão de construção,pode-se afirmar que o numero de quadrados de lado 1 na
vigésima etapa é:
a)758
b)759
c)760
d)761e)762
Obs: Eu tentei resolver pela formula da PA de 2º ordem, usando o numero de quadrados como os elementos. Por exemplo a PA normal seria (1, 5, 13, 25,...) correspondente as 1a, 2a, 3a etc etapas respectivamente! Daí como a razao entre estes elementos gera uma PA de 2a ordem tal que (4, 8, 12,...) de razao constante igual a 4, utilizei a soma dos 20 primeiros termos desta PA de 2a ordem! Mas não deu certo!
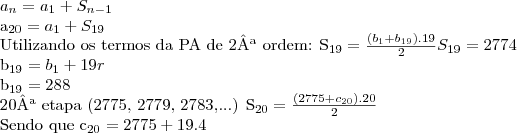
Não acho resultado! Me ajudem!!!!!!!!!!!!!

-
yanagranhen
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jun 17, 2010 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia florestal
- Andamento: cursando
 por Cleyson007 » Seg Jun 21, 2010 22:36
por Cleyson007 » Seg Jun 21, 2010 22:36
Boa noite yanagranhen!
Primeiramente, seja bem vindo (a) ao fórum!
A P.A. segue essa ordem: (1,5,13, ...) segundo sua representação.
Você pode escrever essa mesma P.A. da seguinte forma: (1, 1+4, 1+4+8, ...)
Na vigésima etapa, teremos: (1+4+8+12+16+...an)
Repare que a P.A é constituída a partir do segundo termo (4) - ou seja, são somados 4 a partir do segundo termo.
Achando o termo geral: a19 = a1 + 18r --> a19 = 4 + 18(4) --> a19 = 76
Jogando na fórmula da soma: S = (4 + 76)(19) / 2
Logo, S = 760
A resposta correta não é 760, porque a P.A. é constituída a partir do 1.. mas é importante entender que o 1 faz parte da P.A.
Logo, S = 760 + 1 = 761 (Alternativa d)
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por yanagranhen » Seg Jun 21, 2010 23:16
por yanagranhen » Seg Jun 21, 2010 23:16
Muito obrigada Cleyson007!
Acredita que tava errando multiplicação basica?
É, falta de atenção, devo estar dispersa!
Obrigada!
Abçs
-
yanagranhen
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jun 17, 2010 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia florestal
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PG Termo geral
por apotema2010 » Seg Mar 01, 2010 10:18
- 2 Respostas
- 2102 Exibições
- Última mensagem por apotema2010

Qua Mar 03, 2010 11:10
Progressões
-
- [Termo geral]
por GrazielaSilva » Dom Set 30, 2012 15:24
- 2 Respostas
- 2128 Exibições
- Última mensagem por GrazielaSilva

Qui Out 04, 2012 12:20
Progressões
-
- P.A termo geral
por Brendon » Sáb Fev 16, 2013 14:32
- 2 Respostas
- 3967 Exibições
- Última mensagem por Brendon

Sáb Fev 16, 2013 17:58
Progressões
-
- Mostre que (Termo Geral)
por Cleyson007 » Seg Jul 11, 2011 20:50
- 5 Respostas
- 2495 Exibições
- Última mensagem por LuizAquino

Ter Jul 12, 2011 09:59
Cálculo: Limites, Derivadas e Integrais
-
- [Progressão] Termo Geral da PA
por Jennifer Moreira » Sáb Out 22, 2011 11:20
- 2 Respostas
- 1846 Exibições
- Última mensagem por MarceloFantini

Sáb Out 22, 2011 15:17
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
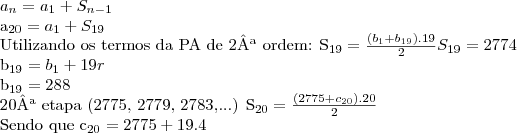







 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.