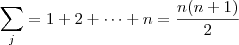 .
. Em seguida , vou deixar minha solução e gostaria de saber como vc's desenvolveriam .
Solução :
 .
. Mas ,
 ou seja
ou seja 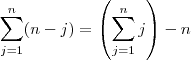 .
. Daí ,
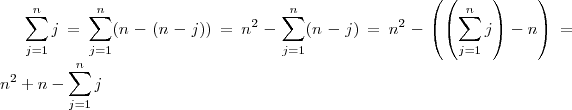 .
. Somando
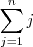 em ambos lados da igualdade vamos obter que ,
em ambos lados da igualdade vamos obter que , 
e finalmente , multiplicando toda igualdade por
 ,
, 
teremos que ,
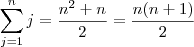 .
. Agora que cheguei no lado direito através do esquerdo , posso provar por indução que vale para n + 1 ou melhor ainda mostro que vale para n-1 e para n+1 .
OBS.: Alguém de vc's conhecem algum livro que posso deparar com exercícios como este acima e também sobre indução matemática .


 . Somando ambas, temos
. Somando ambas, temos 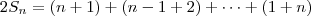 . Ao fazer isto efetuamos
. Ao fazer isto efetuamos  somas, daí
somas, daí 
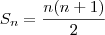 .
.




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.