+
+
"Quais as progressões aritméticas nas quais a soma de dois termos quaisquer faz parte da progressão?"
Se eu tomar dois termos quaisquer: [ap = a1+(p-1)*r] + [aq = a1+(q-1)*r] chego a ap+aq = 2a1+(p+q-1-1)*r mas aí eu "empaco"...a resposta do livro é a1 = k*r, k Inteiro, isto é o primeiro termo da progressão tem que ser múltiplo da razão o que é claro, pois aí qualquer termo será múltiplo de r, assim como a soma de quaisquer termos...só eu não vislumbro os passos de ap+aq = 2a1+(p+q-1-1)*r até a1 = k*r, k Inteiro.
Agradeço uma orientação.
Gratos
Colton
+
+


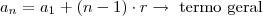
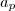 e
e 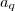 .
.
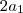 e na do termo geral, apenas
e na do termo geral, apenas 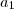 , assim,
, assim,  para que a soma dos dois seja um termo da PA, algo do tipo
para que a soma dos dois seja um termo da PA, algo do tipo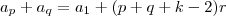 onde
onde 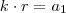 e é claro
e é claro 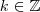 (usei
(usei  para ficar igual à solução do teu livro), afinal não existe o termo
para ficar igual à solução do teu livro), afinal não existe o termo  numa progressão.
numa progressão. algébrica para isso.
algébrica para isso. 

 .
.



