1ª Etapa
?
2ª Etapa
?
???
?
3ªº etapa
?
???
?????
???
?
4ª etapa
?
???
?????
???????
?????
???
?
Seguindo esse padrão de construção,pode-se afirmar que o numero de quadrados de lado 1 na vigésima etapa é:
a)758
b)759
c)760
d)761
e)762
Obs: Eu tentei resolver pela formula da PA de 2º ordem, usando o numero de quadrados como os elementos. Por exemplo a PA normal seria (1, 5, 13, 25,...) correspondente as 1a, 2a, 3a etc etapas respectivamente! Daí como a razao entre estes elementos gera uma PA de 2a ordem tal que (4, 8, 12,...) de razao constante igual a 4, utilizei a soma dos 20 primeiros termos desta PA de 2a ordem! Mas não deu certo!
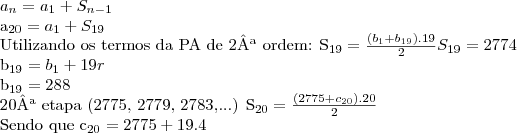
Não acho resultado! Me ajudem!!!!!!!!!!!!!






 .
.
 :
: