 por Carolziiinhaaah » Qua Jun 16, 2010 12:06
por Carolziiinhaaah » Qua Jun 16, 2010 12:06
Calcule a soma da série:
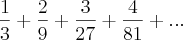
.
gabarito:

-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Qua Jun 16, 2010 13:18
por Elcioschin » Qua Jun 16, 2010 13:18
1/3 + 2/9 + 3/27 + 4/81 + .....
1/3 + (1/9 + 1/9) + (1/27 + 2/27) + (1/81 + 3/81) + .....
(1/3 + 1/9 + 1/27 + 1/81 + ....) + (1/9 + 2/27 + 3/81 + .....)
Soma dos termos do primeiro parenteses é uma PG infinita de razão 1/3 ----> Sa = (1/3)/(1- 1/3) ----> Sa = 1/2
Segundo parenteses ----> 1/9 + 2/27 + 3/81 + .....
1/9 + (1/27 + 1/27) + (1/181 + 2/81) + .....
(1/9 + 1/27 + 1/81 + ....) + (1/27 + 2/81 + .....)
Soma dos termos do primeiro parenteses é uma PG infinta de razão 1/3 ----> Sb = (1/9)/(1- 1/3) ----> Sa = 1/6
Segundo parenteses ----> 1/27 + 2/81 + .......
1/27 + (1/81 + 1/81) + .....
(1/27 + 1/81 + .....) + (1/81 + .....)
Soma dos termos do primeiro parenteses é uma PG infinita de razão 1/3 ----> Sa = (1/27)/(1- 1/3) ----> Sc = 1/18
E assim por diante, teremos ----> S = Sa + Sb + Sc + ...... ----> S = 1/2 + 1/6 + 1/18 + .....
Temos uma nova PG infinta de razão 1/3 -----> S = (1/2)/(1 - 1/3) -----> S = 3/4
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova por Indução (Soma de Progressão)
por RicardoSouza » Sex Fev 17, 2012 20:30
- 4 Respostas
- 4400 Exibições
- Última mensagem por nietzsche

Sex Mar 02, 2012 03:11
Progressões
-
- [progressão Aritmética] sequência com soma
por JKS » Dom Mar 17, 2013 14:16
- 1 Respostas
- 1191 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 15:07
Aritmética
-
- Progressão geométrica (Soma da PG infinita)
por kellykcl » Qui Fev 27, 2014 23:20
- 2 Respostas
- 4058 Exibições
- Última mensagem por alexandre_de_melo

Sex Fev 28, 2014 17:07
Progressões
-
- [Progressão geométrica] Soma dos n primeiros termos
por fff » Ter Jan 07, 2014 13:30
- 3 Respostas
- 5279 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 17:47
Sequências
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4249 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
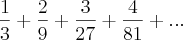 .
.

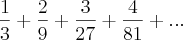 .
.

