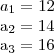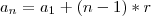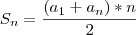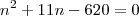por Adriana Baldussi » Qua Abr 14, 2010 16:28
por Adriana Baldussi » Qua Abr 14, 2010 16:28
Tenho 3 problemas sobre PA,com os resultados que tenho que obter.Já tentei de tudo,mas não chego nesse bendito resultado!Ajuda,por favor!
1)Um teatro possui 12 poltronas na primeira fileira,14 na segunda,16 na terceira,e assim por diante.Quantas fileiras são necessárias para o teatro ter um total de 620 poltronas?
Veja se confere:
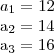
r= 2
Sn=620
n= ?
an= ?
Como não tenho o n nem o an,a professora disse que acharíamos um termo geral,que iria dentro da conta da soma,no lugar de ambos: an e n.
O resultado é 20 fileiras,mas não consigo chegar nisso!
-
Adriana Baldussi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Set 29, 2009 15:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Abr 14, 2010 16:42
por Molina » Qua Abr 14, 2010 16:42
Adriana Baldussi escreveu:Tenho 3 problemas sobre PA,com os resultados que tenho que obter.Já tentei de tudo,mas não chego nesse bendito resultado!Ajuda,por favor!
1)Um teatro possui 12 poltronas na primeira fileira,14 na segunda,16 na terceira,e assim por diante.Quantas fileiras são necessárias para o teatro ter um total de 620 poltronas?
Veja se confere:
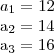
r= 2
Sn=620
n= ?
an= ?
Como não tenho o n nem o an,a professora disse que acharíamos um termo geral,que iria dentro da conta da soma,no lugar de ambos: an e n.
O resultado é 20 fileiras,mas não consigo chegar nisso!
Boa tarde, Adriana.
Você pensou certo. O que faltou era usar a definição de PA:



...
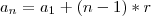
Jogando na fórmula da Soma:
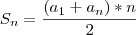



Resolvendo isso vai cair numa equação do 2° grau:
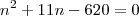
Agora ache as raizes e pegue apenas a positiva!
 PS: Nas próximas dúvidas crie um novo tópico com o seu exercício, e não utilize tópico dos outros para fazer isso. Lembrando que deve ser colocado apenas uma questão por tópico.
PS: Nas próximas dúvidas crie um novo tópico com o seu exercício, e não utilize tópico dos outros para fazer isso. Lembrando que deve ser colocado apenas uma questão por tópico.Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adriana Baldussi » Qua Abr 14, 2010 17:21
por Adriana Baldussi » Qua Abr 14, 2010 17:21
Desculpe,mas é que não estou conseguindo criar um novo tópico,mesmo seguindo as dicas de outros fóruns.
-
Adriana Baldussi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Set 29, 2009 15:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressão aritimetica
por Carlos NI » Qua Abr 22, 2009 23:51
- 1 Respostas
- 1708 Exibições
- Última mensagem por Molina

Qui Abr 23, 2009 00:42
Progressões
-
- [PROGRESSAO ARITIMETICA]
por Alexandrefzs » Seg Dez 16, 2013 23:29
- 0 Respostas
- 1617 Exibições
- Última mensagem por Alexandrefzs

Seg Dez 16, 2013 23:29
Progressões
-
- Ajuda - Progressão Aritimética
por luiz_sky » Ter Jan 12, 2010 22:09
- 4 Respostas
- 3216 Exibições
- Última mensagem por Molina

Seg Fev 22, 2010 13:44
Progressões
-
- [progressao aritimetica] termo de uma p.a
por santtus » Seg Fev 18, 2013 19:33
- 2 Respostas
- 2113 Exibições
- Última mensagem por santtus

Seg Fev 18, 2013 21:31
Progressões
-
- [Progressão Aritimetica] Vento Angulo Força ax ay
por richard1994x » Qua Jan 30, 2013 21:22
- 0 Respostas
- 1378 Exibições
- Última mensagem por richard1994x

Qua Jan 30, 2013 21:22
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.