 por replay » Qui Ago 01, 2013 11:55
por replay » Qui Ago 01, 2013 11:55
(UECE) Seja (a1, a2, a3, a4, a5, a6, a7, a8) uma progressão aritmética. Se a2+a5=8 e a8=7, então a3+a7 é igual a:
a) 8
b) 28/3
c) 10
d) 32/3
Não consigo desenvolver um raciocínio para resolver este problema.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Pessoa Estranha » Sex Ago 02, 2013 15:26
por Pessoa Estranha » Sex Ago 02, 2013 15:26
Olá. Segue o meu raciocínio. Espero que entenda.
Como trata-se de uma progressão aritmética, sabemos que estamos trabalhando em função do primeiro termo (a1) e da razão (podemos chamar de "r"). Observe que o segundo termo, por exemplo, nada mais é do que o primeiro termo somado com a razão. Agora, note que podemos pensar assim também: o terceiro termo, por exemplo, corresponde à soma do primeiro termo com duas vezes a razão (a3 = a1 + 2r) ou à soma do segundo termo com a razão (a3 = a2 + r). E este raciocínio segue sucessivamente. Bem, o enunciado do problema diz que trata-se de uma progressão aritmética e nos traz duas informações importantes:
a2 + a5 = 8 e
a8 = 7. Assim, note que podemos fazer o seguinte:

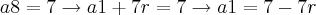
Daí, podemos igualar as duas expressões encontradas. Veja:
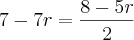
Então:

Daí, como temos o valor da razão, podemos encontrar o valor do primeiro termo:
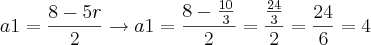
Assim:
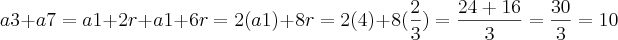
Alternativa C.
Tem o gabarito? Se tiver mande uma resposta dizendo se está correto.
Espero ter ajudado.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Sáb Ago 03, 2013 08:11
por DanielFerreira » Sáb Ago 03, 2013 08:11
Pessoa, encontrei um lapso na sua resolução! Dê uma olhada na parte que destaquei:
Pessoa Estranha escreveu:Olá. Segue o meu raciocínio. Espero que entenda.
Como trata-se de uma progressão aritmética, sabemos que estamos trabalhando em função do primeiro termo (a1) e da razão (podemos chamar de "r"). Observe que o segundo termo, por exemplo, nada mais é do que o primeiro termo somado com a razão. Agora, note que podemos pensar assim também: o terceiro termo, por exemplo, corresponde à soma do primeiro termo com duas vezes a razão (a3 = a1 + 2r) ou à soma do segundo termo com a razão (a3 = a2 + r). E este raciocínio segue sucessivamente. Bem, o enunciado do problema diz que trata-se de uma progressão aritmética e nos traz duas informações importantes:
a2 + a5 = 8 e
a8 = 7. Assim, note que podemos fazer o seguinte:

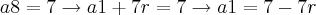
Daí, podemos igualar as duas expressões encontradas. Veja:
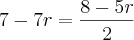
Então:

Daí, como temos o valor da razão, podemos encontrar o valor do primeiro termo:
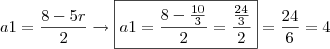
Assim:
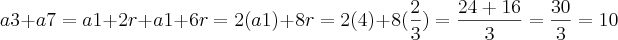
Alternativa C.
Tem o gabarito? Se tiver mande uma resposta dizendo se está correto.
Espero ter ajudado.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Pessoa Estranha » Sáb Ago 03, 2013 11:12
por Pessoa Estranha » Sáb Ago 03, 2013 11:12
Você tem razão. Peço desculpas pelo meu erro grave.
O correto é:
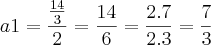

.
Desculpe.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por replay » Sáb Ago 03, 2013 22:54
por replay » Sáb Ago 03, 2013 22:54
Valeu, essa é mesmo a resposta, agora entendi a resolução.
Resposta C: 10
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 02, 2013 09:13
por DanielFerreira » Sáb Nov 02, 2013 09:13
Pessoa Estranha escreveu:Você tem razão. Peço desculpas pelo meu erro grave.
O correto é:
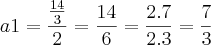

.
Desculpe.

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6128 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4721 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5625 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4418 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8393 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




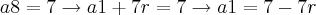
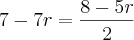

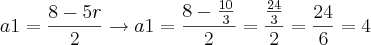
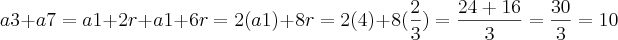


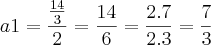
 .
.

.

