Considere os dados apresentados na tabela a seguir, obtidos pelo movimento de um automóvel que se desloca em
linha reta ao longo de uma rodovia.
t(s) 2 5 x 11
d(m) 16 y 196 484
A distância (d), percorrida pelo automóvel, partindo do repouso, é diretamente proporcional ao quadrado do tempo (t).
Considerando-se os valores dados na tabela em questão, o valor de é:
a)47.
b)107.
c)117.
d)97.
na verdade nao tenho certeza se é progressao aritmetica, mas acredito que seja...seguindo essa ideia eu achei o r que é 3, logo x=8 , mas nao consigo achar y... quem sabe eu tenha feito td errado e isso nem seja uma PA, bom, espero que possam me ajudar.


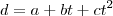 , onde
, onde  ,
,  e
e  são constantes.
são constantes.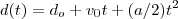 , que é a lei de movimento de um móvel acelerado de
, que é a lei de movimento de um móvel acelerado de  . Supondo que comecemos a contar a distancia a partir de
. Supondo que comecemos a contar a distancia a partir de 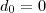 , então
, então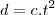
 temos
temos  , de forma que
, de forma que  e , portanto,
e , portanto,  .
. e assim voce pode calcular tanto x quanto y.
e assim voce pode calcular tanto x quanto y.
 [tex]
[tex]