[Progressão Geométrica] Questão interessante.

por **Russman** » Qui Jan 17, 2013 19:19

Achei a questão abaixo interessante principalmente pelo dever de interpretar bem o enunciado e pensei em compartilhar com vocês.

: PG.gif (25.21 KiB) Exibido 1790 vezes

por **ant_dii** » Sex Jan 18, 2013 03:03

Bom,
a função que governa este crescimento é dada fazendo o seguinte: t=tempo em horas e f(t)=numero de bactérias no tempo t
para

temos

$0 \rightarrow 10$
$12 \rightarrow 20$
$24 \rightarrow 40$

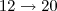
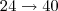
e assim por diante. Toda função exponencial é dada por $f(x)=a \cdot b^x$ .

Fazendo então
$f(0)=a \cdot b^0=10 \Rightarrow a=10$

$f(12)=a \cdot b^{12} = 20 \Rightarrow 10b^{12}=20 \Rightarrow b^{12}=2 \Rightarrow b=2^{\frac{1}{12}}$

temos $f(t)=10 \cdot 2^{\frac{1}{12}t}$

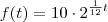
Como se quer saber em 7 dias e dobra a população a cada doze horas, teremos 24*7=168. Então t=168, logo

$f(168)=10 \cdot 2^{\frac{1}{12}168}=10 \cdot 2^{14}$ ...

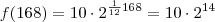
Colocando

$10 \cdot 2^{14}=x$
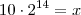
teremos

$\log{(10 \cdot 2^{14})}= \log{x} \Rightarrow \log{10}+\log{2^{14}} = \log{x} \Rightarrow 1+14\cdot \log{2}=\log{x}$

utilizando a aproximação dada teremos

$1+14 \cdot 0,3 =\log{x} \Rightarrow 5,2=\log{x} \Rightarrow 10^{5,2}=x$

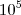
O que indica que o número de bactérias, decorrida uma semana exata e desconsiderando qualquer outro fator, estará entre $10^{5}$ e
$10^{5,5}$ .

por **Russman** » Sex Jan 18, 2013 20:05

Isso mesmo, amigo. :y:

Boa resolução.

Eu comentei sobre o enunciado pois muita gente errou essa questão por fazer confusão na contagem do tempo.

[Progressão Geométrica] Questão interessante.

[Progressão Geométrica] Questão interessante.

[Progressão Geométrica] Questão interessante.

Re: [Progressão Geométrica] Questão interessante.

Re: [Progressão Geométrica] Questão interessante.

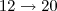
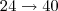
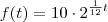
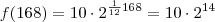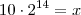
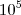Quem está online