Em uma progressão geométrica de seis termos e razão 2, a diferença entre os dois últimos termos é 48.
Qual é o primeiro termo dessa progressão?
(A) 3
(B) 6
(C) 12
(D) 14
(E) 28
A resposta é letra (A), como será que se chega ao resultado? alguém saberia?


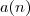 é dado por
é dado por 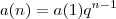 onde
onde  é a sua razão.
é a sua razão. .
. . Assim,
. Assim, 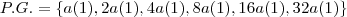 .
.
 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)