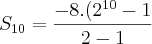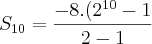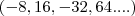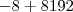por Aprendiz2012 » Sex Out 12, 2012 21:22
por Aprendiz2012 » Sex Out 12, 2012 21:22
Da PG (-8, -16, -32, ..., an) calcule a soma dos 10 primeiros termos.
como fiz:
cheguei em q=2
portanto:
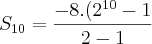
=- 8184
mas no gabarito está S10= 2728
2 elevado a 10 = 1024 - 1 = 1023 x -8 = -8184
não consigo identificar o erro
-
Aprendiz2012
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sáb Ago 11, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em química
- Andamento: formado
 por DanielFerreira » Sex Out 12, 2012 21:34
por DanielFerreira » Sex Out 12, 2012 21:34
Sua resposta está correta!

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Aprendiz2012 » Sex Out 12, 2012 22:12
por Aprendiz2012 » Sex Out 12, 2012 22:12
Nossa.. então o meu gabarito está errado mesmo??
obrigado aí...=)
-
Aprendiz2012
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sáb Ago 11, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em química
- Andamento: formado
 por young_jedi » Sex Out 12, 2012 22:37
por young_jedi » Sex Out 12, 2012 22:37
como o nosso amigo danjr5 ja mostrou sua resposta esta correta mais eu
acredito que oque esteja errado é a PG do enunciado
se ela fosse
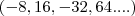
resolvendo provavelmente voce chegara nesta resposta do gabarito
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Aprendiz2012 » Ter Out 16, 2012 02:13
por Aprendiz2012 » Ter Out 16, 2012 02:13
Obrigado mesmo... excelente..
-
Aprendiz2012
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sáb Ago 11, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em química
- Andamento: formado
 por replay » Ter Out 16, 2012 19:27
por replay » Ter Out 16, 2012 19:27
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Out 16, 2012 19:31
por young_jedi » Ter Out 16, 2012 19:31
replay
voce pode sim fazer a distributiva dessa maneira
A unica coisa é que voce se esqueceu do denominador -1 nas duas primeiras passagens e colocou depois.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por replay » Ter Out 16, 2012 19:36
por replay » Ter Out 16, 2012 19:36
young_jedi escreveu:replay
voce pode sim fazer a distributiva dessa maneira
A unica coisa é que voce se esqueceu do denominador -1 nas duas primeiras passagens e colocou depois.
Não sei se é recomendando mas as vezes faço isso pra poupar espaço.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Out 16, 2012 19:44
por young_jedi » Ter Out 16, 2012 19:44
se voce consegue entender tudo o que esta sendo feito, e quiser separar a equação por partes não vejo problema nenhum, a questão é que as vezes agente acaba esquecendo de algo que foi deixado de fora antes e ai acaba não fazendo o exercicio direito, outra coisa é que fazendo todos os passos certinho fica facil de alguem de fora acompanhar, alem do que quando voce se acustuma a fazer as coisas de um jeito informal depois quando tem que fazer de maneira formal acaba tendo dificuldade.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por replay » Ter Out 16, 2012 19:46
por replay » Ter Out 16, 2012 19:46
Vou fazer completo, valeu pela dica. É que sou meio relaxado mesmo.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Aprendiz2012 » Sex Out 19, 2012 02:46
por Aprendiz2012 » Sex Out 19, 2012 02:46
é caras.. meu cérebro por exemplo não funciona direito na questão de organização, se eu não colocar todos os detalhes.. sempre esqueço depois... no meu caderno coloco até as contas com detalhes adicionais e explicações com palavras.. mas como você está na internet, certamente quis poupar digitação.
-
Aprendiz2012
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sáb Ago 11, 2012 18:07
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em química
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11054 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10764 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12526 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3154 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5723 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.