(Mackenzie) Se a sequência (2, 1/2, 4, 1/4, 6, 1/8, ...) é formada por termos de uma progressão aritmética alternados com os termos de uma progressão geométrica, então o produto do vigésimo pelo trigésimo primeiro termo dessa sequência é:
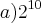

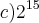

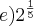
Percebi que os termos da P.A. ficam em posições ímpares.
então a posição 31 é uma P.A, e a posição 20 é uma P.G.
Cãlculo da P.A.

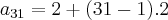
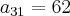
____________________________________________
Cálculo da P.G.
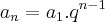

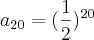
___________________________________________
Soma


Não sei se até onde fiz esta certo, mas também não sei como resolvo a soma, não tem como fatorar 62 para deixar com base 1/2
Valeu!


 para os termos ímpares;
para os termos ímpares; para os termos pares.
para os termos pares. e
e 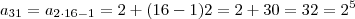 .
.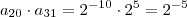 .
.


 (pares) e para considerar as equações de progressão geométrica você deve levar em conta que apenas os termos com índice da forma
(pares) e para considerar as equações de progressão geométrica você deve levar em conta que apenas os termos com índice da forma  (ímpares).
(ímpares). .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
