 por LuRodrigues » Dom Abr 22, 2012 20:22
por LuRodrigues » Dom Abr 22, 2012 20:22
Encontrei a questão a seguir e não estou conseguindo estruturar a resolução:
Uma bola de borracha cai de uma altura h. Após chocar-se com o solo atinge uma altura igual a 2/3 da anterior e esta lei se mantém nos choques subsequentes. Pergunta-se: quanto a bola terá percorrido até que pare?
Do problema, extrai:
a1=h
an=0
q=2/3
n=?
s=?
Acredito que seja preciso considerar a "subida" e "descida" a cada choque da bola, mas ao utilizar a fórmula da soma dos termos de PG finita, não encontro a resposta 5h. Poderiam me ajudar?
-
LuRodrigues
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 22, 2012 19:03
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por Edu-sjc » Seg Abr 23, 2012 16:05
por Edu-sjc » Seg Abr 23, 2012 16:05
Este problem não dá pra ser resulvido direto, você temm que resolve-lo em suas partes, que seguem:
i) Primeiro vamos fazer a soma das das altura atingidas após a primeira colisão com o chão, que nos dá a seguinte sequêcia:

onde,
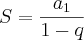
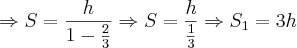
ii) Agora a somas das "quedas" da bola des de h, que noa dá a seguinte sequência:


Somando os espasos de subida S1 e de decida S2 vamos te 5h.
Espero ter ajudado !!!
-
Edu-sjc
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Out 26, 2011 12:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Ter Mai 01, 2012 01:05
por DanielFerreira » Ter Mai 01, 2012 01:05
Atente a
i), note que

então,
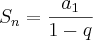
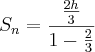
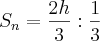


Daí, 2h + 3h =
5h"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz em um sub-espaco!?
por tsigwt » Sex Ago 22, 2008 23:09
- 1 Respostas
- 2478 Exibições
- Última mensagem por admin

Sáb Ago 23, 2008 23:52
Álgebra Linear
-
- Espaço vetorial
por amr » Sex Abr 01, 2011 15:30
- 4 Respostas
- 8207 Exibições
- Última mensagem por Rosi7

Sáb Mai 30, 2015 00:16
Introdução à Álgebra Linear
-
- Reta no espaço
 por Phisic » Qui Jul 21, 2011 13:58
por Phisic » Qui Jul 21, 2011 13:58
- 8 Respostas
- 4364 Exibições
- Última mensagem por Phisic

Seg Jul 25, 2011 10:05
Álgebra Elementar
-
- CONICAS NO ESPACO
por celestepaixao » Dom Nov 13, 2011 11:43
- 3 Respostas
- 1808 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 21:10
Geometria Analítica
-
- G A Distancia Espaço
por joaozer » Ter Abr 24, 2012 22:19
- 1 Respostas
- 1265 Exibições
- Última mensagem por joaozer

Ter Abr 24, 2012 23:07
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



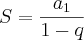
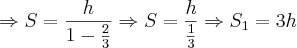



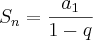
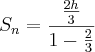
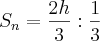





 , avisa que eu resolvo.
, avisa que eu resolvo.

