I - Se x e y são números reais positivos então
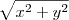 =
=  .
.II - Para quaisquer números reais x e y, tem-se
 .
.III - A igualdade
 vale para quaisquer números reais não nulos x e y.
vale para quaisquer números reais não nulos x e y.IV - Se x é um número real tal que
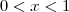 então
então 
Pode-se dizer que:
a) Apenas uma afirmação é verdadeira.
b) Apenas duas afirmações são verdadeiras.
c) Apenas três afirmações são verdadeiras.
d) Todas as afirmações são verdadeiras.
Cálculo
I - Se x e y são números reais positivos então
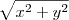 =
=  .
.![\displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y \displaystyle \sqrt[2]{x^2+y^2} = \sqrt[\not 2]{x^{ \not 2}} + \sqrt[ \not 2]{y^{ \not 2}} = x + y](/latexrender/pictures/b72c6a7039de78fa463d388da31963a1.png)
1ª Afirmação Verdadeira.
II - Para quaisquer números reais x e y, tem-se
 .
.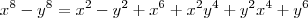
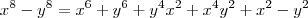
Logo,

2ª Afirmação Falsa.
III - A igualdade
 vale para quaisquer números reais não nulos x e y.
vale para quaisquer números reais não nulos x e y.
3ª Afirmação Falsa.
IV - Se x é um número real tal que
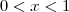 então
então 
Se 0 < x < 1 , logo
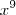 é < que
é < que 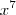
Logo, 4ª Afirmação Falsa
Resposta Certa Letra A: Apenas uma afirmação é verdadeira.
Eu não sei se eu acertei no cálculo e também não possuo o gabarito da questão, espero que possam me ajudar.
Desde já Agradeço!

-----------
Obs.: Primeira Postagem no Fórum!




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.