 são definidos por:
são definidos por: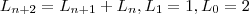 .
.a. Prove que, para todo n maior ou igual a 0,
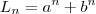 , onde
, onde 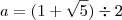 e
e 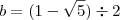
b. Prove que
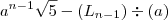 é um número de Lucas, para cada n>0
é um número de Lucas, para cada n>0c. Prove que
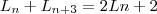 , para todo n maior ou igual a 0.
, para todo n maior ou igual a 0.Não tenho ideia de como se faz isso se alguém puder me ajudar, obrigado.

 são definidos por:
são definidos por: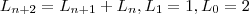 .
.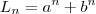 , onde
, onde 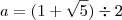 e
e 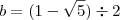
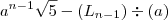 é um número de Lucas, para cada n>0
é um número de Lucas, para cada n>0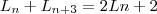 , para todo n maior ou igual a 0.
, para todo n maior ou igual a 0.
MateusDantas1 escreveu:Para cada n inteiro positivo, os números de Lucas L_n são definidos por:,
,
.
a. Prove que, para todo n maior ou igual a 0,, onde
e
b. Prove queé um número de Lucas, para cada n>0
c. Prove que, para todo n maior ou igual a 0.
MateusDantas1 escreveu:Não tenho ideia de como se faz isso
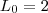
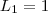
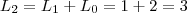
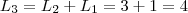
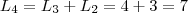
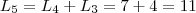
MateusDantas1 escreveu:a. Prove que, para todo n maior ou igual a 0,, onde
e
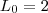 .
.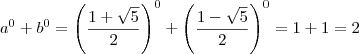
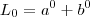
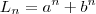
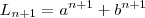
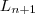 .
.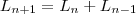
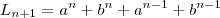
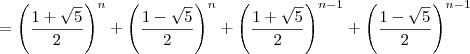
![= \left(\dfrac{1+\sqrt{5}}{2}\right)^n\left[1 + \left(\dfrac{1+\sqrt{5}}{2}\right)^{-1}\right] + \left(\dfrac{1-\sqrt{5}}{2}\right)^n\left[1 + \left(\dfrac{1-\sqrt{5}}{2}\right)^{-1}\right] = \left(\dfrac{1+\sqrt{5}}{2}\right)^n\left[1 + \left(\dfrac{1+\sqrt{5}}{2}\right)^{-1}\right] + \left(\dfrac{1-\sqrt{5}}{2}\right)^n\left[1 + \left(\dfrac{1-\sqrt{5}}{2}\right)^{-1}\right]](/latexrender/pictures/8ede39b9901405f8fc3ee0d7dd2bb062.png)
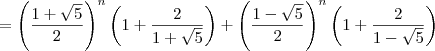
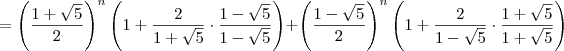
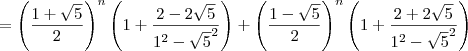
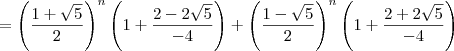
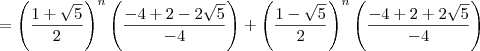
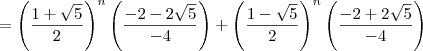
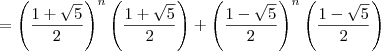
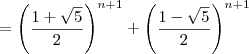
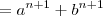
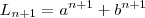
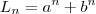 , onde
, onde 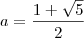 e
e 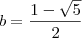 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



